Math of the Rundetaarn

As we were exiting the Rundetaarn (“Round Tower”) in Copenhagen, Denmark, I noticed a man wearing a shirt with the following quotation:

Find what you love, and let it kill you.

The only problem is that the shirt attributed the quotation to poet Charles Bukowski, when apparently it should have been attributed to humorist Kinky Friedman. For what it’s worth, my favorite Friedman quote is, “I just want Texas to be number one in something other than executions, toll roads, and property taxes.” But this ain’t a post about Kinky Friedman, or even Charles Bukowski. So, allow me to pull off the sidewalk and get back on the boulevard.

Whoever said it, the quotation hit me as drastically appropriate. I suspect that math will someday kill me… likely as I cross the street while playing KenKen on my phone, oblivious to an oncoming truck. As I exited the Rundetaarn, I was thinking about all the math that I had seen inside — much of which, I suspect, would not have been seen by many of the other tourists.

The Rundetaarn, completed in 1642, is known for the 7.5-turn helical ramp that visitors can walk to the top of the tower and, coincidentally, to one helluva view of the city. 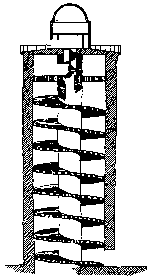That leads to Question #1.

Along the outer wall of the tower, the winding corridor has a length of 210 meters, climbing 3.74 meters per turn. What is the (inside) diameter of the tower?

Above Trinitatis Church is a gift shop that is accessible from the Rundetaarn’s spiral corridor. The following clock was hanging on the wall in that little shop:

I have no idea who the bust is, but the clock leads to Question #2.

What sequence of geometric transformations were required to convert a regular clock into this clock?

And to Question #3.

Do the hands on this clock spin clockwise or counterclockwise?

And to Question #3a.

What is the “error” on the clock?

A privy accessible from the spiral corridor in the Rundetaarn has been preserved like a museum exhibit. Sadly, I have no picture of it to share, but a sign next to the privy implied that the feces deposited by a friar would fall 12 meters into the pit below.

That leads to Question #4.

What is the terminal velocity of a deposit when it reaches the bottom of the pit? (Or should that be “turd-minal velocity”?)

The first respondent to correctly answer all of these questions will earn inalienable bragging rights for perpetuity.