I’d Like a Wordle with You

Okay, fine, if no one else will say it, then I’ll say it: Wordle is a pain-in-the-ass.

I know, I know. It’s probably political suicide to denigrate the most popular word game on the planet, but if speaking truth to power means I’ll never be the Archbishop of Canterbury or a member of the Delaware Chancery Court, well, so be it.

There are two aspects of Wordle that are a tempest in a teacup:

• First, solving the puzzle in just one or two guesses is largely a matter of luck. In and of itself, this is not a problem. Rather, it’s the braggarts on social media who ascribe their success to intelligence rather than serendipity that really grinds my gears.
• Second, the Wordle app contains a fundamental flaw. If life intervenes and causes you to miss a day — perhaps because you’re on a canoe trip with no internet service; or, you’re visiting Green Bank, West Virginia, where cell phones and wi-fi are illegal; or, you’re perilously close to proving the Riemann hypothesis and are afraid to pause and lose focus — then your Wordle streak is reset and you’re required to begin anew. Personally, I think the streak should only reset if (a) you fail to find the word in six guesses or (b) you fail to find the word using one or more guesses before the next puzzle appears on the following day.

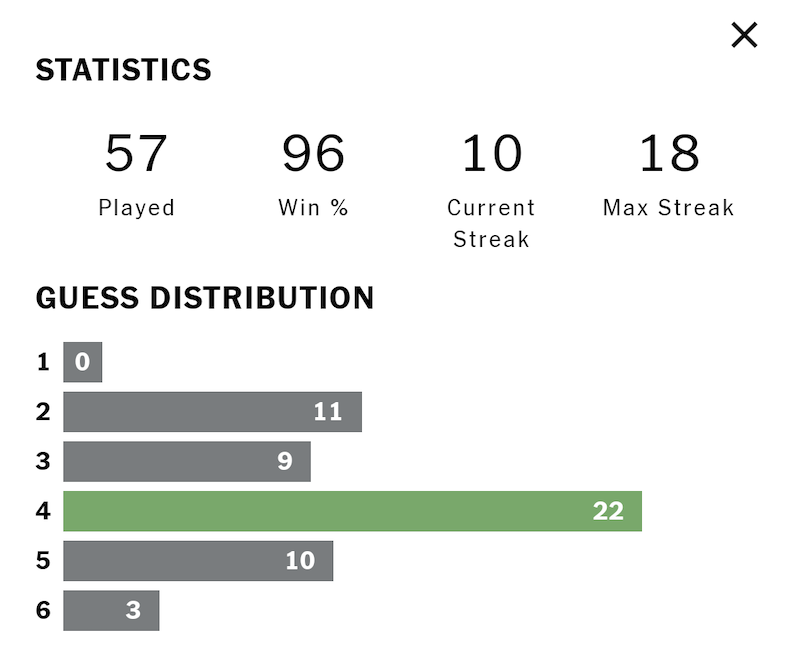
For me, there is no joy in finding the word in just two guesses; but, there is utter devastation if the correct answer isn’t found in six guesses. Sadly, I’ve twice failed to find the word:

This, of course, leads to a math problem:

As shown above, I’ve played 313 games, and I’ve solved 5 + 59 + 158 + 72 + 17 = 311 of them. Consequently, the Wordle app displays my Win % as 99. Assuming typical rules of rounding, how many puzzles will I need to solve (without a miss) so that it displays my Win % as 100?

My wife takes great joy in finding the word in just two guesses, so for her, occasionally failing to solve the puzzle in six tries is a fair tradeoff. But her risky strategy means that her Win % suffers a bit:

Though I’ve played six times as many games, she’s solved the puzzle in two guesses more than twice as many times as I have.

But despite its imperfections, I’m still addicted to Wordle.

One of the reasons is that the statistics surrounding Wordle permit interesting birdwalks for math geeks. To wit, the Wordle database allegedly contains 12,545 allowable words but only 2,309 possible answers. If you randomly guess one of the allowable words, you have a 0.008% chance of finding the word on your first guess; instead, if you randomly guess one of the possible answers, you have a 0.04% change of finding the word on your first guess. So, how have Wordle players been able to guess the answer on their first try more than 0.02% of the time?

Another reason for my addiction is my love of anagrams.

For your puzzling pleasure, here are some anagram puzzles for you. The first is about my favorite four-letter anagrams.

The letters S, T, O, and P can be combined to form 24 different arrangements. Amazingly, six of them are actual English words! Can you find them all?

The next four puzzles all have to deal with anagrams of names.

The name CAMERON has only one anagram, but oh, what a beautiful word! Can you find it?

The letters of the name ANDREW can be rearranged to create three other words. Can you find all three?

When I meet someone new, I take it as a personal challenge to find an anagram of their name. Sometimes, though, an anagram just doesn’t exist. Which of the following names cannot have its letters rearranged to form a common English word?

• ANNIE
• ARTIE
• BRIAN
• CARSON
• DEEPAK
• DANIEL
• ELISA
• LISA
• MATTHEW
• NEVAEH
• TIARET

(This is a true story.) A mother named ANIDA wrote to babynames.com and said she planned to give a name to each of her children that was an anagram of her own name. How many can you come up with? Admittedly, some of her suggestions aren’t terribly common. But what’s in a name, anyway? (Head to babynames.com to see her letter and her list of names.)

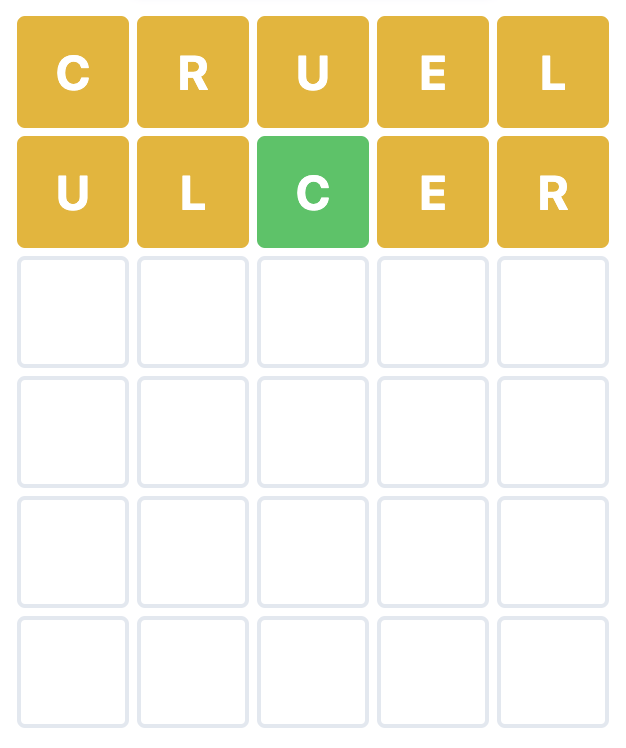
Finally — but not least importantly — allow me to introduce you to the Make Your Own Wordle generator at Strive Math. Using that site, some five‑letter anagrams were used to show a few Wordle games already in progress. For each of the puzzles below, you should be able to get the word on the next guess. (Amazingly, there are six possible anagrams of the letters A, E, L, S, and T for Puzzle 3, but the answer is uniquely determined after just these two guesses.)

Puzzle 1. Three guesses, three correct letters. What’s the word?

Puzzle 2. Two guesses, one correct letter. What’s the word?

Puzzle 3. Two guesses, zero correct letters. What’s the word?

The six anagrams of S, T, O, and P are OPTS, POST, POTS, SPOT, STOP (duh!), and TOPS.

ROMANCE is the only anagram of CAMERON.

The letters of ANDREW can be rearranged to form WANDER, WARDEN, and WARNED.

Only MATTHEW can’t be rearranged to form a common English word. (If you can’t find anagrams of the others, use the oldest and, in my opinion, the best anagram generator on the web.)

The letters of ANIDA can be arranged to make quite a few names: AIDAN, DIANA, DAIAN, NADIA, DANIA, DAINA, ADINA, NAIAD, and probably many others.

And the three Wordles are solved with NOTES, LUCRE, and STEAL.

See you in three months, when I’ll hopefully be able to display a Win % of 100.

Math Puzzles with Letters

This week on the NPR Sunday Puzzle, host Will Shortz offered the following challenge:

Name a famous city in ten letters that contains an s. Drop the s. Then assign the remaining nine letters their standard value in the alphabet — A = 1, B = 2, C = 3, etc. The total value of the nine letters is only 25. What city is it?

It’s not much of a spoiler to note that the average value of those nine letters must be less than three, since their sum “is only 25.” Consequently, a lot of those letters must occur at the beginning of the alphabet and — if eight of them were a‘s — there would be no letters later than q in the name of the city. But that’s as much as I’ll say; you can solve the puzzle on your own. (When you do, you can submit your answer for a chance to play next week’s on-air puzzle live with Will Shortz.)

Mathematician Harold Reiter uses a similar problem with elementary school students. Using the same idea — that each letter has a value (in cents) equal to its position in the alphabet — he asks students to find a dollar word, that is, a word whose letters have a sum of 100. As it turns out, there are many. Based on a nonexhaustive search, there are at least 3,500 dollar words, and likely a whole lot more. In a quick perusal of the list, one word jumped out: oxygon. Nope, that’s not a typo. It’s an archaic term meaning “a triangle with three acute angles.”

All of this talk of letters reminds me of my favorite puzzle, which I call Product Values. Using the same scheme — that is, A = 1, B = 2, C = 3, etc. — find the product value of a word by multiplying the values of the letters. So, for instance, cat has a product value of 3 × 1 × 20 = 60. How many words can you find that have a product value of 100? Based on the ENABLE word list, there are nine. (If you need some help, you can use the Product Value Calculator at www.mathjokes4mathyfolks.com.)

To end this post, a few math jokes that involve letters:

And Satan sayeth, “Let’s put the alphabet in math.” Bwa-ha-ha-ha-ha.

Romans had no trouble with algebra, because X was always equal to 10.

Change the Vowel

The following puzzle contains a clue within each clue. The answer, of course, fits the clue, but each answer is also one of the words within the clue with its vowel sound changed. For instance, the clue “the distance from the top of your hat to the sole of your shoes” contains the word hat, and if you change the vowel sound from a short a to a long i, you get height, which fits the description.

As always, there’s a catch. Every answer to the clues below is a mathy word.

1. The number of permutations of three different colored socks.
   
2. This value is the same for 3 + 1 and 2 + 2.
3. Do this with two odd numbers and you’ll get an even number.
4. Three hours before noon.
5. You may fail to correctly expand (a + b)(c + d) if you don’t remember this mnemonic.
6. One represents this fractional portion of toes on the hoof of a deer.
7. The last element of a data set arranged in descending order.
8. The measure of central tendency made from the most common data points.
9. The number of contestants ahead of third place if there’s a tie for first place.
10. If the leader is forced to drop out of a race, the runner-up takes over this place.
11. The square root is needed to calculate the length of the hypotenuse in this type of triangle.
12. The graph of the declination of the Sun during a year can be approximated by this type of curve.

Answers

1. six
   
2. sum
3. add
4. nine
5. FOIL
6. half
7. least
8. mode
9. two
10. first
11. right
12. sine

Mathy Portmanteaux

The term portmanteau was first used by Humpty Dumpty in Lewis Carroll’s Through the Looking Glass:

Well, ‘slithy’ means “lithe and slimy” and ‘mimsy’ is “flimsy and miserable.” You see, it’s like a portmanteau — there are two meanings packed up into one word.

Interestingly, the word portmanteau itself is also a blend of two different words: porter (to carry) and manteau (a cloak).

Portmanteaux are extremely popular in modern-day English, and new word combinations are regularly popping up. Sometimes, perhaps, there are too many being coined. In fact, one author refers to these newcomers as portmonsters, a portmanteau of, well, portmanteau and monster that attempts to capture how grotesque some of these beasts are. An abridged list of portmonsters would include sharknado, arachnoquake, blizzaster, snowpocalypse, Brangelina, Bennifer, Kimye, Javanka, fantabulous, and ridonkulous.

These are Portman toes, not portmanteaux.

Portmanteaux seem to proliferate most easily in B-movie titles, weather, and celebrity couples, but the world of math and science is not free from them. Here are a few mathy portmanteaux, presented, of course, as equations.

ginormous = giant + enormous, really big

guesstimate = guess + estimate, a reasonable speculation

three-peat = three + repeat, to win a championship thrice

clopen set = closed + open set, a topological space that is both open and closed

bit = binary + digit, the smallest unit of measurement used to quantify computer data

pixel = picture + element, a small area on a display screen; many can combine to form an image

voxel = volume + pixel, the 3D analog to pixel

fortnight = fourteen + night, a period of two weeks

parsec = parallax + second, an astronomy unit equal to about 3.26 light years

alphanumeric = alphabetical + numeric, containing both letters and numerals

sporabola = spore + parabola, the trajectory of a basidiospore after it is discharged from a sterigma

gerrymandering = Elbridge Gerry + salamander, to draw districts in such a way as to gain political advantage (In the 1800’s, Governor Elbridge Gerry redrew districts in Massachusetts to his political benefit. One of the redrawn districts looked like a salamander.)

megamanteau = mega + portmanteau, a portmanteau containing more than two words, such as DelMarVa, a peninsula that separates the Chesapeake Bay from the Atlantic Ocean and includes parts of Delaware, Maryland, and Virginia

meganegabar = mega + negative + bar, the line used on a check so that someone can’t add “and one million” to increase the amount

(By the way, when Rutgers University invited Jersey Shore cast member Snooki Polizzi to speak to students on campus in 2011, they paid her $32,000, which is $2,000 more than they paid Nobel and Pulitzer Prize winning author Toni Morrison to deliver a commencement address six weeks later.)

More HIPE

Nearly five years ago, I wrote about HIPE, a parlor game in which one person gives a particular string of letters, and the other people in the parlor try to guess a word with that same string of letters (consecutively, and in the same order).

Well, I recently rediscovered Can You Solve My Problems? by Alex Bellos, and I was pleasantly surprised to find that he included four HIPEs in that book:

1. ONIG
2. HQ
3. RAOR
4. TANTAN

The fourth is one that I had included in my previous post, Don’t Believe the HIPE, and all are good enough that they deserve wide distribution.

Just for fun, here’s a new list of HIPEs that might prove interesting.

• SSP
• LWE
• NUSCU
• CUU
• CTW
• KGA
• UIU
• XII

In an effort to collect a bunch of excellent HIPEs, I’m asking for your help. If you play the game with friends and discover a particularly delectable combination of letters, please share below or at https://forms.gle/otddCw1uLeDALrMo7.

Math Words for National Dictionary Day

Want to start today the right way? Say, “Good morning!” to Alexa today, and she’ll respond:

Good morning! It’s National Dictionary Day. Ever wonder what the shortest word is? Technically, it’s a toss-up between the single letter words I and a, but since I is always capitalized, I’d say a is just a little shorter.

Is there anything more powerful than a language arts joke to get the day off to a good start?

I have no words to describe today. I do, however, have a ton of obscene gestures.

So, what’s the shortest math word? Technically, e and i, but if you don’t like constants, then you’ll have to settle for the three-letter words set and box.

And what’s the longest math word — at least based on the list at Math Words? It has 17 letters, and you’ll get a big hint if you check the time.

What two math words, both having the same number of letters, are equally appropriate to describe a triangle whose sides are congruent?

And what’s the funniest math word? Personally, I think it’s syzygy, but according to Tomas Engelthaler, it’s logic. In Humor Norms for 4,997 English Words, Engelthaler and Hills (2017) describe a method for determining which words are funniest. I emailed Engelthaler to ask which math word is funniest, and he responded as if it were a completely reasonable question. Without hesitation, he shared a list of math words and their humor rankings, and these five were at the top of the list:

• logic
• math
• theory
• science
• graph

The overall funniest English word, according to Engelthaler’s research? Booty. Go figure.

While you may not think that any of those words, mathy or otherwise, are laugh-out-loud funny, this isn’t debatable; it’s based on science.

If you take issue with this research, you’ll need to discuss it with Engelthaler and his colleagues. Please write to him directly to say that you’re bumfuzzled, that his research is malarkey, or that you think he’s a nincompoop.

Friday Word Puzzle

Sometimes, a small word is contained in a longer word. For example, you can see the three-letter word rid tucked nicely inside Friday in the title for this post, and zip can be found in the middle of marzipan.

Some folks have told me that the following word-in-a-word is particularly appropriate for this blog…

…since my puns put the UGH in LAUGHTER.

Words within words are the basis of today’s puzzle.

Complete each of the nine words below by placing a three-letter word in the blank. The three-letter words that you use all belong to the same category. But there is a tenth three-letter word from the same category that is not used below. What is the category, and what is the missing word?

1. OB _ _ _ D
2. C _ _ _ PY
3. M _ _ _ OT
4. PH _ _ _ M
5. H _ _ _ SE
6. VE _ _ _ D
7. CA _ _ _ OU
8. EL _ _ _ SE
9. LE _ _ _ E

When I started to create this puzzle, I was hoping to give you a similar list in which a short math word was found in a longer word. I found several, but they seem pretty darn hard, and the missing words aren’t always obviously mathy. But for fun, you can try your hand at these, too…

1. D _ _ _ Y
2. AS _ _  _ E
3. SE _ _ _ H
4. BU _ _ _ _ SS
5. EL _ _ _ _ TH
6. C _ _ _ _ RA
7. RU _ _ _ _ NT
8. SH _ _ _ _ BLE
9. BRA _ _ _ _ ILD
10. HU _ _ _ _ D
11. PR _ _ _ _ _ IFY
12. RE _ _ _ _ NT
13. WA _ _ _ _ ELON
14. DE _ _ _ _ OR
15. HO _ _ _ _ SS
16. H _ _ _ _ HOG
17. IM _ _ _ _ ST

 

---

ANSWERS

1. OB eye D
2. C hip PY
3. M arm OT
4. PH leg M
5. H ear SE
6. VE toe D
7. CA rib OU
8. EL lip SE
9. LE gum E

The three-letter words are all parts of the body. The tenth word in that category is jaw, which never appears in the interior of a longer word (only at the beginning or end, such as jawbone or lockjaw).

1. D add Y
2. AS sum E
3. SE arc H
4. BU sine SS
5. EL even TH
6. C hole RA
7. RU dime NT
8. SH area BLE
9. BRA inch ILD
10. HU more D
11. PR equal IFY
12. RE side NT
13. WA term ELON
14. DE mean OR
15. HO line SS
16. H edge HOG
17. IM mode ST

Dos Equis XX Math Puzzles

No, the title of this post does not refer to the beer. Though it may be the most interesting blog post in the world.

It refers to the date, 10/10, which — at least this year — is the second day of National Metric Week. It would also be written in Roman numerals as X/X, hence the title of this post.

For today, I have not one, not two, but three puzzles for you. I’m providing them to you well in advance of October 10, though, in case you’re one of those clever types who wants to use these puzzles on the actual date… this will give you time to plan.

The first is a garden-variety math problem based on the date (including the year).

Today is 10/10/16. What is the area of a triangle whose three sides measure 10 cm, 10 cm, and 16 cm?

Hint: A triangle appearing in an analogous problem exactly four years ago would have had the same area.

The next two puzzles may be a little more fun for the less mathy among us — though I’m not sure that any such people read this blog.

Create a list of words, the first with 2 letters, the second with 3 letters, and so on, continuing as long as you can, where each word ends with the letter X. Scoring is triangular: Add the number of letters in all the words that you create until your first omission. For instance, if you got words with 2, 3, 4, 5, and 8 letters, then your score would be 2 + 3 + 4 + 5 = 14; you wouldn’t get credit for the 8-letter word since you hadn’t found any 6- or 7-letter words.

2 letters: _________________________
3 letters: _________________________
4 letters: _________________________
5 letters: _________________________
6 letters: _________________________
7 letters: _________________________
8 letters: _________________________
9 letters: _________________________
10 letters: _________________________
11 letters: _________________________
12 letters: _________________________
13 letters: _________________________
14 letters: _________________________

Note: There are answer blanks above for words up to 14 letters, because — you guessed it — the longest English word that ends with an X contains 14 letters.

The third and final puzzle is a variation on the second.

How many words can you think of that contain the letter X twice? (Zoiks!) Scoring: Ten points for the first one, and a bazillion points for each one thereafter — this is hard! Good luck!

If you’re in desperate need of help, you can access my list of words for both puzzles — of which I’m fairly proud, since my list of words that end in X include math words for 2 through 10 letters — or do a search at www.morewords.com.

Sound Smart with Math Words

When law professor Richard D. Friedman appeared in front of the Supreme Court, he stated that an issue was “entirely orthogonal” to the discussion. Chief Justice John G. Roberts Jr. stopped him, saying, “I’m sorry. Entirely what?”

“Orthogonal,” Friedman replied, and then explained that it meant unrelated or irrelevant.

Justice Antonin Scalia was so taken by the word that he let out an ooh and suggested that the word be used in the opinion.

In math class, orthogonal means “at a right angle,” but in common English, it means that two things are unrelated. Many mathematical terms have taken a similar path; moreover, there are many terms that had extracurricular meanings long before we ever used them in a math classroom. Average is used to mean “typical.” Odd is used to mean “strange” or “abnormal.” And base is used to mean “foundation.” To name a few.

The stats teacher said that I was average, but he was just being mean.

You know what’s odd to me? Numbers that aren’t divisible by 2.

An exponent’s favorite song is, “All About the Base.”

Even words for quantities can have multiple meanings. Plato used number to mean any quantity more than 2. And forty used to refer to any large quantity, which is why Ali Baba had forty thieves, and why the Bible says that it rained for forty days and forty nights. Nowadays, we use thousands or millions or billions or gazillions to refer to a large, unknown quantity. (That’s just grammatical inflation, I suspect. In a future millennium, we’ll talk of sextillion tourists waiting in line at Disneyland or of googol icicles hanging from the gutters.)

Zevenbergen (2001) provided a list of 36 such terms that have both math and non-math meanings, including:

• angle
• improper
• point
• rational
• table
• volume

The alternate meanings can lead to a significant amount of confusion. Ask a mathematician, “What’s your point?” and she may respond, “(2, 4).” Likewise, if you ask a student to determine the volume of a soup can, he may answer, “Uh… quiet?”

It can all be quite perplexing. But don’t be overwhelmed. Sarah Cooper has some suggestions for working mathy terms into business meetings and everyday speech. Like this…

For more suggestions, check out her blog post How to Use Math Words to Sound Smart.

If you really want to sound smart, though, be sure to heed the advice of columnist Dave Barry:

Don’t say: “I think Peruvians are underpaid.”
Say instead: “The average Peruvian’s salary in 1981 dollars adjusted for the revised tax base is $1452.81 per annum, which is $836.07 below the mean gross poverty level.”
NOTE: Always make up exact figures. If an opponent asks you where you got your information, make that up, too.

This reminds me of several stats jokes:

• More than 83% of all statistics are made up on the spot.
• As many as one in four eggs contains salmonella, so you should only make three-egg omelettes, just to be safe.
• Even some failing students are in the top 90% of their class.
• An unprecedented 69.846743% of all statistics reflect an unjustified level of precision.

You can see the original version of “How to Win an Argument” at Dave Barry’s website, or you can check out a more readable version from the Cognitive Science Dept at Rensselaer.

---

Zevenbergen, R. (2001). Mathematical literacy in the middle years. Literacy Learning: the Middle Years, 9(2), 21-28.

NPR Puzzle Combinations

During yesterday’s NPR Sunday Puzzle, puzzlemaster Will Shortz presented the following challenge:

I’m going to give you some five-letter words. For each one, change the middle letter to two new letters to get a familiar six-letter word. For example, if I said FROND, F-R-O-N-D, you’d say FRIEND, because you’d change the O in the middle to I-E.

He then presented these nine words:

• EARLY
• TULIP
• MOURN
• JUROR
• FUTON
• DEITY
• PANDA
• SLOTH
• VISOR

You can figure out the answers for yourself. For those that give you real trouble, you can either listen to the broadcast or search for the answer at More Words.

For those of you who don’t know who Will Shortz is, you have something in common with detective Jake Peralta from Brooklyn Nine-Nine:

The puzzle was fun. But what was more fun was the conversation that our family had about it. After the third word, Alex announced, “This shouldn’t be that hard. There are only 676 possible combinations.”

What he meant is that there are 26 × 26 = 676 possible two-letter combinations, which is true.

He continued, “But you can probably stop at 675, because Z-Z is pretty unlikely.”

I smiled. He had chosen to exclude Z-Z but not Q-K or J-X or V-P.

Yet his statement struck me as a challenge. Is there a five-letter word where the middle letter could be replaced by Z-Z to make a six-letter word? Indeed, there are several:

• BUSED or BUSES
• CONED or CONES
• FETED
• FUMED or FUMES
• GUILE
• MEMOS
• NOBLE
• PITAS
• RAVED or RAVES
• ROVED or ROVER or ROVES
• TAPAS
• WIDEN
• WINED or WINES

None of them are perfect, though, because Z-Z is not a unique answer. For instance, ROVER could become ROBBER, ROCKER, ROMPER, ROSTER, or ROUTER, and most puzzle solvers would surely think of one of those words before arriving at ROZZER (British slang for a police officer).

From the list above, the best option is probably GUILE, for two reasons. First, stumbling upon GUZZLE as the answer seems at least as likely as the alternatives GUGGLE, GURGLE, and GUTTLE. Second, the five-letter hint has only one syllable, but the answer has two, and such a shift makes the puzzle just a little more difficult.

But while Alex had reduced the field of possibilities to 675, the truth is that the number was even lower. The puzzle states that one letter should be “changed to two new letters,” which implies that there are only 25 × 25 = 625 possibilities. Although that cuts the number by 7.5%, it doesn’t help much… no one wants to check all of them one-by-one to find the answer.

When Will Shortz presented DEITY, the on-air contestant was stumped. So Will provided some help:

I’ll give you a tiny, tiny hint. The two letters are consonant, vowel.

Alex scrunched up his brow. “That’s not much of a hint,” he declared.

Ah, but it is — if you’re using brute force. To check every possibility, this reduces the number from 625 to just 21 × 5 = 105, which is an 80% reduction.

Still, Alex is correct. The heuristic for solving this type of puzzle is not to check every possibility. Rather, it’s to think of the word as DE _ _ TY, and then check your mental dictionary for words that fit the pattern. It may help to know that the answer isn’t two consonants, but most puzzle solvers would have suspected as much from the outset. In the English language, only SOVEREIGNTY, THIRSTY, and BLOODTHIRSTY end with two consonants followed by TY.

Below are five-letter math words for which the middle letter can be changed to two new letters to form a six-letter word. (Note that the answers aren’t necessarily mathy.)

DIGIT :: DI _ _ IT (unique)

POINT :: PO _ _ NT

FOCUS :: FO _ _ US

MODEL :: MO _ _ EL (unique)

POWER :: PO _ _ ER

RANGE :: RA _ _ GE (unique)

SOLID :: SO _ _ ID (unique)

SPEED :: SP _ _ ED

And below, your challenge is reversed: Find the five-letter word that was changed to form a six-letter math word.

CO _ EX :: CONVEX (unique)

LI _ AR :: LINEAR (unique)

OR _ IN :: ORIGIN

RA _ AN :: RADIAN (unique)

SE _ ES :: SERIES

SP _ RE :: SPHERE

Enjoy!