Constant Change

I’m frustrated.

I’m also old, cranky, and cynical. Whatever.

My frustration is not the my-flight-was-delayed-three-times-then-eventually-cancelled-and-there-are-no-more-flights-to-Cleveland-till-tomorrow-morning type. It’s not even the can’t-believe-my-boss-is-making-me-go-to-Cleveland kind of frustration. More like the why-aren’t-there-the-same-number-of-hot-dogs-and-buns-in-a-pack variety. So it’s a First World problem, to be sure, but still annoying. I’ll explain more in a moment.

But first, how ’bout a math problem to get us started?

If you make a purchase and pay with cash, what’s the probability that you’ll receive a nickel as part of your change?

Sure, if you want to get all crazy about this, then we can take all the fun out of this problem by stating the following assumptions:

• You only pay with paper currency. If you paid with coins, then the distribution of coins you’d receive as change would likely vary quite a bit.
• You never use 50¢ coins. Honestly, they’re just too obscure.
• Transaction amounts are uniformly distributed, so that you’re just as likely to receive 21¢ as 78¢ or any other amount.
• Cashiers don’t round because they dislike pennies. So, if you’re supposed to get 99¢ change, the cashier doesn’t hand you a dollar and say, “Don’t worry about it.” Instead, you actually get 99¢ change.

But stating assumptions is a form of mathematical douchebaggery, isn’t it? (As an aside, check out the definition of douchey that’s returned when you do a search. Sexist, anyone?) I prefer problems with no assumptions stated; let folks make their own assumptions to devise a model. If you and I get different answers because of different assumptions, no worries. Maybe we both learn something in the process.

Anyway, where was I? Oh, yeah…

Understanding the solution to that problem is a precursor to the issue that’s causing me frustration. I’ll give the solution in a minute, so pause here if you want to solve it on your own, but let me now allow the proverbial cat out of its bag and tell you why I’m frustrated.

At our local grocery store, there’s a coin counting machine that will count your change, sort it, and spit out a receipt that you can take to the customer service desk to exchange for paper currency. Walk in with a jar full of change, walk out with a fistful of fifties. Pretty nifty, right? Except the machine charges a ridiculous 8.9% fee to perform this service. No, thank you.

My bank used to have a similar coin counting machine, and if you deposited the amount counted by the machine into your account, there was no fee. The problem is that everyone was doing this to avoid the grocery store fee, so the machine broke often. The bank finally decided the machine wasn’t worth the maintenance fees and got rid of it. Strike two.

Which brings me to my current dilemma. One Saturday morning every month, we now spend 30 minutes counting coins and allocating them to appropriate wrappers. Which is fine. The problem, however, is that we run out of quarter and penny wrappers way faster than we run out of nickel or dime wrappers. Which brings me to the real question for the day:

Since pennies, nickels, dimes, and quarters are not uniformly distributed as change, why the hell does every package of coin wrappers contain the same number for each coin type?

The Royal Sovereign Assorted Coin Preformed Wrappers is the best-selling collection of coin wrappers on Amazon, and it provides 54 wrappers for each coin type. They also offer a 360‑pack with 90 wrappers for each coin type; Minitube offers a 100‑pack with 25 wrappers for each coin type; and Coin-Tainer offers a 36‑pack with 9 wrappers for each coin type. But what no one offers, so far as I can tell, is a collection of coin wrappers with a distribution that more closely resembles the distribution of coins that are received as change.

Whew! It feels good to finally raise this issue for public consideration.

So, the question that I really wanted to ask you…

Given the distribution of quarters, dimes, nickels, and pennies that are received in change, and given the number of coins needed to fill a coin wrapper — 40 quarters, 50 dimes, 40 nickels, and 50 pennies — how many of each wrapper should be sold in a bundled collection?

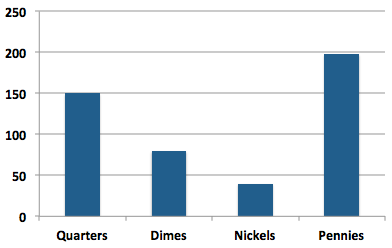
To answer this question, I determined the number of coins of each type required for every amount of change from 1¢ to 99¢. The totals yield the following graph:

The number of pennies is nearly five times the number of nickels. And there are nearly twice as many quarters as dimes.

But I realize that’s a theoretical result that may not match what happens in practice, since this assumes that the amounts of change from 1¢ to 99¢ are uniformly distributed (they aren’t) and that cashiers don’t round down to avoid dealing with pennies (they do). In fact, when I made a purchase of $2.59 yesterday, instead of getting one penny, one nickel, one dime, and one quarter as change, the cashier gave me one penny, three nickels, and one quarter, in what was clearly a blatant attempt to skew my data.

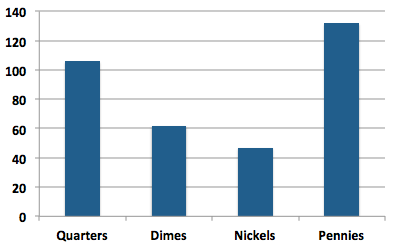
So for an experimental result, I counted the pennies, nickels, dimes, and quarters in our home change jar. The results were similar:

The ratio of pennies to nickels is closer to three, but the ratio of quarters to dimes is still roughly two.

Using a hybrid of the theoretical and experimental results, and accounting for the fact that only 40 quarters and nickels are needed to fill a wrapper whereas 50 pennies and dimes are needed, it seems that an appropriate ratio of coin wrappers would be:

quarters : dimes : nickels : pennies :: 17 : 8 : 6 : 19

Okay, admittedly, that’s a weird ratio. Maybe something like 3:2:1:4, to keep it simple. Or even 2:1:1:2. All I know is that 1:1:1:1 is completely insane, and this nonsense has got to stop.

Hello, Royal Sovereign, Minitube, and Coin-Tainer? Are you listening? I’ve completed this analysis for you, free of charge. Now do the right thing, and adjust the ratio of coin wrappers in a package accordingly. Thank you.

---

Wow, that was a long rant. Sorry. If you’ve made it this far, you deserve some comic relief.

How many mathematicians does it take to change a light bulb?
Just one. She gives it to a physicist, thus reducing it to a previously solved problem.

If you do not change direction, you may end up where you are heading. – Lao Tzu

The only thing that is constant is change. – Heraclitus

Turn and face the strange ch-ch-ch-changes. – David Bowie

A Buddhist monk walks into a Zen pizza parlor and says, “Make me one with everything.” The owner obliged, and when the pizza was delivered, the monk paid with a $20 bill. The owner put the money in his pocket and began to walk away. “Hey, where’s my change?” asked the monk. “Sorry,” said the owner, “change must come from within.”

---

As for the “probability of a nickel” problem that started this post, here’s my solution.

For change amounts from 1¢ to 25¢, there are ten values (5‑9 and 15‑19) for which you’ll receive a nickel as part of your change.

This pattern then repeats, such that for change amounts from 25n + 1 to 25n + 25, where n is the number of quarters to be returned, you’ll receive a nickel when the amount of change is 25n + k, where k ∈ {5, 6, 7, 8, 9, 15, 16, 17, 18, 19}. For 0 ≤ n < 4, there are 40 different amounts of change that will contain a nickel, so the probability of getting a nickel as part of your change is 40/100, or 40%.

Heavy Cookies, Undervalued Coins, and Misconceptions

Simple question to get us started…

Which is worth more?

And of course the answer is, “The quarters, because 50¢ is more than 20¢,” right? But not to a kindergarten student or a pre-schooler who hasn’t yet learned how much coins are worth. A young student might argue, “Four is more than two.”

Why didn’t the quarter follow the nickel when he rolled himself down the hill?
Because the quarter had more cents.

Recently, I was asked to review an educational video for kindergarten math that had a similar question.

The video stated, “Can you tell the green, yellow, and orange cookies are heavier? That makes sense, doesn’t it? Because there are more of them!”

Uh, no.

This is the same logic that would lead one to claim that the value of four nickels is greater than the value two quarters because there are more nickels. It’s a huge misconception for students to focus on number rather than value. So it’s very frustrating to see this video reinforce that misconception.

For example, if each green, yellow, or orange cookie weighs 3 ounces, but each blue or purple cookie weighs 5 ounces, then the left pile would weigh 6 × 3 = 18 ounces, and the right pile would weigh 4 × 5 = 20 ounces, so the right side would be heavier. (Then again, are there really 6 cookies on the left and 4 on the right, or are some cookies hidden? Hard to tell.)

As far as I’m concerned, the only acceptable answer is that the pile of green, yellow, and orange cookies must be heavier — assuming, of course, that the balance scale isn’t malfunctioning — because the pans are tipped in that direction.

All of this reminds me of the poem “Smart” by Shel Silverstein.

SMART

My dad gave me one dollar bill
‘Cause I’m his smartest son,
And I swapped it for two shiny quarters
‘Cause two is more than one!

And then I took the quarters
And traded them to Lou
For three dimes — I guess he don’t know
That three is more than two!

Just then, along came old blind Bates
And just ’cause he can’t see
He gave me four nickels for my three dimes,
And four is more than three!

And I took the nickels to Hiram Coombs
Down at the seed-feed store,
And the fool gave me five pennies for them,
And five is more than four!

And then I went and showed my dad,
And he got red in the cheeks
And closed his eyes and shook his head–
Too proud of me to speak!

Dreidel is Not Fair

play an online version of dreidel at the Jewish Outreach Institute (but turn the sound off)

Is dreidel fair?

The rules of dreidel are straightforward. At the beginning of each round, players put one coin into the pot. (For young kids, the “coins” are actually chocolate pieces in the shape of a coin and wrapped in gold foil. This is known as geld, and as far as I’m concerned, chocolate is a currency to kids.) Players then take turns spinning the dreidel, and a reward is earned based on which of the four Hebrew letters appears on top when the dreidel stops spinning:

• Nun: nothing.
• Hey: half the pot.
• Gimel: all of the pot.
• Shin: put one in.

Play continues clockwise, with each person spinning the dreidel until Gimel occurs and all coins are removed from the pot. At that point, everyone antes another coin, and a new round starts with the next player.

Officially, a player is out of the game when she or he has no coins left to contribute to the pot, and the game ends when one person has all the coins. But practically speaking, the game often ends much earlier, because players get bored and quit or, in the case of very young kids, the game lasts beyond bedtime and the children are pulled away by their parents.

No matter how the game ends, though, it’s not fair.

The following table is courtesy of Paul J. Nahin (Will You Be Alive 10 Years from Now?, Princeton University Press, 2014, p. 81). It shows the amount, over the long run, that each player will win during a dreidel game.

		Player
		1	2	3	4	5
Number of Players	2	1.143	0.857
	3	1.361	0.956	0.680
	4	1.617	1.102	0.757	0.524
	5	1.900	1.267	0.855	0.580	0.398

In other words, the first player has a significant advantage over the others. In a game of five players who start with 10 coins each, the first player will finish the game with 19 coins, on average, whereas the fifth player will finish with just 4 coins. That’s if the game ends early. If played until one person gets all the coins, then the first player is five times more likely to win than the fifth player.

This disparity in odds is likely the reason that an unofficial rule of dreidel is that the youngest player goes first, the second-youngest player goes second, and so on.

The word dreidel is Yiddish and means “to turn around.” Because the dreidel is, after all, a top.

This fact is not lost on comedian Lewis Black, who has some thoughts on the matter.

Happy Chanukah!

Math on Monday Night Football

Tonight’s Eagles-Panthers game had several mathematical incidents.

A Counting Problem

During pre-game warm-ups, a voice-over quoted one of the player’s thusly:

You want me to describe playing on Monday night in one word? Prime time.

Computer scientists start counting at 0. Apparently pro football players start counting at 2.

Speaking of counting… did you notice that the sentence above had three hyphenated words? That’s just crazy.

Flippin’ Out

During the opening kick-off, Mike Tirico mentioned that the Carolina Panthers lost the coin toss. That alone is not exceptional, but it was the eleventh straight game that they had lost the flip. The odds of a team being that unlucky? How about 2,047 to 1?

Perhaps they can blame bad luck for their eight losses this season, too.

Numerically Interesting Milestone

Wide receiver Steve Smith of the Panthers caught a pass in the first half that took him to 745 career receptions for a total of 11,011 yards. What a cool number! First, it’s a palindrome. Second, 11011₂ = 27₁₀, and he currently ranks 27th among wide receivers in career receiving yards. That’s a pretty fun coincidence.

Kicking Off Could Become Flipping Off in NFL

One of the most exciting plays in the history of professional (American) football was the opening play of the second half of Super Bowl XLIV, when the New Orleans Saints recovered an onside kick. They then scored to take a 13–10 lead, and eventually won the game 31–17.

But onside kicks could be a thing of the past. Yesterday, New York Giants’ co-owner John Mara suggested that kickoffs might someday be eliminated from the NFL. This caused a lot of sports pundits to react, saying that it would inherently change the game. On the Mike and Mike Show, analyst Mark Schlereth responded with these rhetorical questions:

What’re you gonna do, flip a coin three times in a row? You gotta get heads three times in a row to get an onside kick?

Once again, probability was placed front-and-center in recent football discussions. While I like Schlereth’s new, less violent, and more mathematical approach to onside kicks, I just wish he had gotten the math right.

If you flip three coins, the probability of getting three heads is 12.5%. That’s not enough. Data shows that onside kicks in the NFL are successful 26% of the time. So the following would be a reasonable modification to Schlereth’s proposal:

Flip two coins. Two heads results in a successful onside kick.

Then the probability would be 25%, closer to the current reality.

Unfortunately, that’s not exactly right, either — it’s based on a misleading statistic. The success rate of onside kicks is highly dependent on whether the team receiving the kickoff is expecting it or not. When teams are expecting it, the success rate hovers around 20%; when teams aren’t expecting it, however, the success rate jumps to 60%. Considering that data, the process might be modified as follows:

1. Kicking team indicates to referee that they will try an onside kick.
   • Of course, this must be done secretly, so as not to arouse the suspision of the receiving team. I propose that one referee be assigned to each team; the team would encode the message using RSA encryption, and the assigned referee would be given the corresponding RSA numbers. A message can then be passed without fear of interception by the receiving team. To ensure that this procedure does not signficantly delay the game, messages stating “we WILL try an onside kick” and “we WILL NOT try an onside kick” could be prepared in advance, and unemployed math PhD’s could be hired as NFL referees to decode the messages.
2. The receiving team must similarly indicate whether or not they suspect an onside kick.
   • Again, use RSA encryption.
3. If the kicking team chooses an onside kick, and the receiving team suspects an onside kick, then:
   • Flip 9 coins. If 9, 8, 3, or 1 of them land heads, the onside kick is successful.
   • P(9, 8, 3, or 1 head with 9 coins) = 20.1%
4. If the kicking team chooses an onside kick, but the receiving team does not suspect it, then:
   • Flip 9 coins. If 9, 8, 5, 4, or 2 of them land heads, the onside kick is successful.
   • P(9, 8, 5, 4, or 2 heads with 9 coins) = 60.0%
5. If the kicking team does not choose an onside kick, then:
   • Flip 9 coins, just so the receiving team is unaware of what the kicking team decided to do, which will allow for the element of surprise with future kicks.

If the NFL decides to accept Mark Schlereth’s suggestion for using coins to determine onside kicks, I am hopeful that they will give my proposal serious consideration. If necessary, I have an Excel spreadsheet that I would be willing to share with them.

Football Math for Super Bowl Week

Super Bowl week seems an appropriate time to share some jokes that involve football and math.

[Super Bowl Squares Online Contest]

What is this?

B
BA
BACK

Here’s another one involving fractions. (And that lead-in should be a hint if you had trouble with the question above.)

What do you call a Patriots fan with half a brain?
Gifted!

And just to be an equal opportunity offender…

What did the average Giants player get on his Wonderlic test?
Drool.

There are several one-liners involving football and math (sort of).

Pro football players are so huge, it takes only four of them to make a dozen.

Their nickel defense is only worth 3¢.

His uniform number was 29, which was also his house number. He wore it to make sure he remembered where to go after the game.

That last one reminded me of a mathy football joke involving dumb people…

By the time Bubba arrived to the football game, the first quarter was almost over. “Why are you so late?” his friend asked.

“I tossed a coin to decide between going to church or coming to the game.”

“I don’t understand. How long could that have taken?”

“Well,” Bubba said, “I had to toss it 14 times.”

For a similar, non-football coin-tossing joke, read the one about the student at the final exam.

Dollar Nim

The following post was featured at the NYTimes Numberplay blog during the week of August 8‑15, 2011.

One-Pile Nim (a.k.a., Static Nim) is a game in which there is a pile of n objects, and each player can take up to k objects on her turn. The player who removes the last object wins. For example, on the TV show Survivor: Thailand in October 2002, the contestants were given an “immunity challenge” in which there were 21 flags, and a team could remove 1, 2, or 3 flags on a turn. (Using the notation above, n = 21 and k = 3.) Avinash Dixit claims that “the actual players [on Survivor: Thailand] got almost all of their moves wrong,” but the strategy for winning this game is not terribly difficult to figure out. If you’re not familiar with the game, you might enjoy determining the strategy on your own, so I won’t spoil your fun.

While riding back from a camping trip yesterday, my wife was keeping my sons amused by playing mental math games with them. However, she was using mostly drill-and-kill exercises, where she would state an expression like 21 – 6, and one of them would shout, “15!” Before I was able to suggest that she play a game that involved more strategy and less rote mathematics, she offered the following.

• Start with $1, or with 100¢, if you prefer.
• On alternating turns, players can remove any coin they like. (Well, technically, players remove a number of cents equal to the value of one of the four common U.S. coins — quarter, dime, nickel, penny — but such an overly complicated statement of the rules would have confused my sons.)
• The player who reduces the value to 0¢ wins.

That is, n = 100, and a player must choose to remove a value from the set {1, 5, 10, 25}.

I was duly impressed by my wife’s creation. (By “my wife’s creation,” I mean to refer to the game she made up, not to my sons, though the moniker would be equally applicable to the latter, and I must admit that I am often duly impressed by my sons, too.) It was a version of Nim that I had never seen before, and the optimal strategy was not obvious to me. Moreover, it had the characteristics of activities that I love to use with young kids: it causes them to practice some useful basic skill (in this case, calculating change for a dollar) for the purpose of trying to win a strategy game with more sophisticated mathematics.

My two sons, my wife, and I played Dollar Nim several times. During our third game, my wife took a dime to leave me with 29¢. “Daddy’s going to win,” Alex declared. Sure enough, I took a quarter to leave 4¢, and the outcome was decided. Both Alex and Eli had realized that if one of us was able to reduce the amount to 4¢, that person would win — everyone would be forced to take a penny.

Analyzing this game for two players is not terribly difficult, though once I had done it, I was intrigued by the patterns that appear in the optimal strategy. Analyzing the game for four players is a bit more difficult.

In the post on the NYTimes NumberPlay blog, Pradeep Mutalik offered the following extension question:

Since Dollar Nim is played with real money, it makes sense for the participants to keep the change they remove. This confers a reward for removing larger denominations. To offset this, the winner must be given an extra monetary reward. What should be the minimum prize money for the two-player game so that no matter what happens, the winner comes out ahead?

I’ll leave it as an exercise for the reader to determine the optimal strategy for the two- and four-player versions of this game, as well as to determine the answer to Pradeep’s question.

[Update, 6/30/11] The sequence of “unsafe” values for two-player Dollar Nim is now listed as A192333 in the Online Encyclopedia of Integer Sequences.

Infinite Gifts

A mathematician came across a lamp. He rubbed it, and a genie appeared. “Can I have three wishes?” asked the mathematician.

The genie had decided long ago that granting three wishes for his release was passé, and he generally refused such requests. With the holidays just around the corner, however, he was feeling charitable. “Okay, fine,” he said. “But agreeing to grant you three wishes takes care of your first wish, so you have only two remaining.”

The mathematician thought for a moment. It sure would be helpful to have a little extra money with which to buy gifts for my friends and family, he thought. “Okay,” said the mathematician, “I’d like a coin bag that is always full of gold; no matter how many gold coins I remove, there will always be some left.”

“Done,” said the genie as he handed the mathematician a coin bag.

The mathematician tried it out and, sure enough, no matter how many coins he removed from the bag, it always remained full. He was absolutely delighted.

“So, then, what would you like for your third wish?” asked the genie.

“Ah, well, that coin bag is awesome,” said the mathematician. “In fact, it’s so good, I’d like another one just like it!”