When a Half Is More Than a Half (and When It Ain’t)

Tonight, the dreadful Philadelphia Eagles defeated the pathetic New York Giants 22‑21 in a match-up of horrendous one-win teams. But not all one-win teams are created equal: in late September, the Eagles played the Bengals to a 23‑23 tie in a game that might have featured the all-time worst ending ever. As a result, the Eagles entered tonight’s game with a horrid 1‑4‑1 record, but not to be outdone, the Giants entered the game with a slightly more putrid 1‑5 record.

In football, a tie counts as a half-win (and a half-loss). But half-wins are sometimes worth more than half a win, sometimes they’re worth less than half a win, and sometimes they’re worth exactly half a win. Let me ‘splain.

After their win tonight, the Eagles record is 2‑4‑1. For the time being, that puts them atop the lowly NFC East:

Eagles	2-4-1
Cowboys	2-4
Washington	1-5
Giants	1-6

 

Philadelphia has played 7 games and won 2 1/2 of them. That is, they’ve won

of their games. That puts them ahead of Dallas, who has won

of their games. So, the Eagles are currently in first place by 1/42 of a game.

But let’s say the Eagles had entered tonight with a 3‑2‑1 record and the Cowboys were 4‑2. After tonight’s win, the Eagles would be 4-2-1, and they would’ve won

of their games. The Cowboys, on the other hand, would have won

of their games, and the Cowboys would be leading the division by 1/42 of a game.

So that half-win tie? It’s worth more to the Eagles because they’re terrible. Were they at least mediocre, that tie wouldn’t be as valuable.

On the other hand, if the Eagles had entered tonight with a 2‑3‑1 record and the Cowboys were 3‑3, then the Eagles would have been 3-3-1 after tonight’s win, and they would’ve won

of their games. Similarly, the Cowboys would have won

of their games, and the teams would’ve been tied for first in the pitiful, talentless, miserable NFC East.

(Yes, I’m being hard on the NFC East, but it isn’t unwarranted. The average power ranking of the four teams is 28, when the lowest possible is 30.5. The four starting quarterbacks have thrown nearly as many interceptions as touchdowns (24 TDs, 22 Ints), and the four teams’ top running backs have more fumbles than touchdowns (11 TDs, 12 Fum). Seriously, this division may be all-time bad.)

All that said, it’s highly unlikely that the season will end with the Eagles having played more games than the Cowboys. Then again, with COVID‑19, who knows what might happen?

It’s often been said that football is “a game of inches.” But given the importance of half-wins, isn’t it time we started saying that football is “a game of fractions”?

Interactions with Fractions

This math factoid, compliments of Learn Fun Facts, is just too good not to share…

Ah, but maybe you missed it. Did you notice that each digit 1-9 appears exactly once in all three fractions? Pretty cool. But I have to say that this is still my favorite fraction equation:

Simple. Beautiful.

On the other hand, I’m not sure I have a favorite fraction joke. I mean, how do you pick just one? The number of fraction jokes is a lot like

.

That’s right. There’s no limit.

5 out of 4 people have trouble with fractions.

I will express polynomials as partial fractions. I will compute the value of continued fractions. I will even find a least common denominator. But I draw the line between the numerator and denominator.

What is one-fifth of a foot?
A toe.

How many tents can fit in a campground?
Ten, because ten tents (tenths) make a whole!

Before you go, here’s a fun little fraction problem for you:

What is 1/2 of 2/3 of 3/4 of 4/5 of 500?

The Homework Inequality: 1 Great Problem > 50 Repetitive Exercises

Yesterday, my sons Alex and Eli were completing their homework on fraction operations, which included 39 problems in 4 sets, wherein each problem in a set was indistinguishable from its neighbors.

The worksheet contained 12 problems of fraction addition, 9 problems of fraction subtraction, 9 problems of fraction multiplication, and 9 problems of fraction-times-whole-number multiplication. That’s 39 problems of drudgery, when 10 problems would’ve been sufficient. Here’s a link to the worksheet they were given, if you’d like to torture your children or students in a similar way:

Lesson 0.1: Adding and Multiplying Fractions

Frustrated by the monotony of the assignment, I told the boys they didn’t have to do all of the problems, and they could stop when they felt that they had done enough from each set.

“No,” said Alex. “We’re supposed to do them all.”

My sons are responsible students, but I’m frustrated by teachers who take advantage of their work ethic. Just because they’re willing to complete 50 exercises for homework doesn’t mean they should be assigned 50 exercises for homework.

My colleague at Discovery Education, Matt Cwalina, puts it this way:

Some say that a picture is worth a thousand words. I say,

A great problem is worth a thousand exercises.

Personally, I would much rather have students think deeply about one challenging problem than mindlessly complete an entire worksheet. Luckily, my sons take after their daddy and love number puzzles, so I spontaneously created one.

Find three fractions, each with a single-digit numerator and denominator, that multiply to get as close to 1 as possible. Don’t repeat digits.

Eli started randomly suggesting products. “What about 4/5 × 6/7 × 9/8?” He’d work out the result, say, “I think I can do better,” then try another. And another. And another. Finally, he found a product that equaled 1. (No spoiler here. Find it yourself.)

Alex eventually found an answer, too. At the bottom of his homework assignment, he added a section that he titled “Bonus” where he captured his attempts:

I don’t know exactly how many calculations Eli completed while working on this problem, but I know that Alex completed at least seven, thanks to his documentation. Wouldn’t you agree that completing several fraction computations while thinking about this more interesting problem is superior to doing a collection of random fraction computations with no purpose?

There is a preponderance of evidence (see Rohrer, Dedrick, and Stershic 2015; definitely check out Figure 4 at the top of page 905) that massed practice — that is, completing a large number of repetitions of the same activity over and over — is counterproductive. Unfortunately, massed practice feels good because it results in short-term memory gains, which trigger a perceived level of mastery; but, it doesn’t lead to long-term retention. Moreover, students who learn a skill by practicing it repeatedly get really good at performing that skill when they know it’s coming; but, two months down the road, when they need to use that skill in an unfamiliar context because it’s not on a worksheet titled “Lesson 0.1: Adding and Multiplying Fractions,” they’re less likely to remember than if they had used more effective practice methods. One of those more effective methods is interleaving, which involves spacing out practice over multiple sessions and varying the difficulty of the tasks. Whether you’re trying to learn how to integrate by parts or how to hit a curve ball, be sure to make your practice exercises a little more difficult than you’re used to. Know that interleaving your practice will not feel as good as massed practice while you’re doing it; but later, you’ll feel better due to improved memory, long-term learning, and mastery of skills.

Interleaving is one of the reasons I love the MathCounts School Handbook, which can be downloaded for free from the MathCounts website. The topics covered by the 250 problems in the School Handbook run the gamut from algebra, number sense, and probability, to geometry, statistics, combinatorics, sequences, and proportional reasoning — and any given page may contain problems of any type! Veteran MathCounts coach Nick Diaz refers to this mixture as “shotgun style,” meaning that students never know what’s coming next. Consequently, similar problems are not presented all at once; instead, students are exposed to them several days or perhaps weeks apart. Having to recall a skill that hasn’t been used for a while requires more effort than remembering what you did just five minutes ago, but the result is long-term retention. It’s doubtful that the writers of the first MathCounts School Handbook knew the research about interleaving and massed practice… but they clearly knew about effective learning.

The other reason I like the MathCounts School Handbook is the difficulty level of the problems. Sure, some of the items look like traditional textbook exercises, but you’ll also find a lot of atypical problems, like this one from the 2017-18 School Handbook:

If p, q, and r are prime numbers such that pq + r = 73, what is the least possible value of p + q + r?

That problem, as well as the fraction problem that I created for Alex and Eli, would both fall into the category of open-middle problems, which means…

• the beginning is closed: every students starts with the same initial problem.
• the end is closed: there is a small, finite number of unique answers (often, just one).
• the middle is open: there are multiple ways to approach and ultimately solve the problem.

Open-middle problems often allow for implicit procedural practice while asking students to focus on a more challenging problem. This results in a higher level of engagement for students. Moreover, it reduces the need for massed practice, because students are performing calculations while doing something else. You can find a large collection of open-middle problems at www.openmiddle.com, and the following is one of my favorites:

Use the digits 1 to 9, at most one time each, to fill in the boxes to make a result that has the greatest value possible.

It’s a great problem, because random guessing will lead students to combinations that work, but it may not be obvious how to determine the greatest possible value. Consequently, there’s an entry point for all students, the problem offers implicit procedural practice, and the challenge of finding the greatest value provides motivation for students to continue.

I have a dream that one day, in traditional classrooms where 50 problems are assigned for homework every night, where procedural fluency is valued over conceptual understanding; that one day, right there in those classrooms, students will no longer think that math is simply a series of disparate rules with no purpose, but instead will experience the joy of attempting and solving challenging problems that inspire purposeful play and, as a side benefit, encourage students to practice the skills they will need to be successful learners.

There are myriad resources available so that teachers and parents can encourage their students to engage in these kinds of problem-solving activities, so it is my hope that this dream is not too far away.

---

As a special bonus for reading to the end, check out this Interleaved Mathematics Practice Guide that Professor Doug Rohrer was kind enough to share with me (and now, with you).

Fractional Fun

It’s well known that 5 out of 4 people have trouble with fractions, but even the mathematically advanced may have a little trouble with this puzzle. Your challenge is simple…

Find the sum of all items in the following table.

A hint is below the table, and the answers are below that. Good luck!

 

Hmm… it seems that you scrolled down here a little too quickly for the hint. Try harder. To put some distance between you and the hint, here are some fraction jokes:

How is sex like a fraction?
It’s improper for the larger one to be on top.

Which king invented fractions?
Henry the Eighth.

There’s a fine line between the numerator and denominator.
(And it’s called a vinculum.)

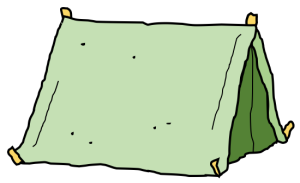
Okay, you’ve waited long enough. Here’s your hint. The items in the table are a fird (fish + bird), wooden forts, bottles of whiskey, the Sith lord Darth Maul, wraiths, and tents. (By the way, thanks to www.HikingArtist.com for the cool drawing of the fird!) Hope that helps.

To put some space between the hint and the answer, here are some more fraction jokes:

A student once told me, “To prove to you that I understand equivalent fractions, I only did three-sevenths of my homework.”

I was scared half to death… twice.

What is one-fifth of a foot?
A toe.

Okay, you’ve waited (and endured) enough. Without further adieu, the answer is 2.5. The images in the table are:

• one fird
• two forts
• four fifths
• one Sith
• four wraiths
• two tents

the sum of which is

.

You’re welcome.

Thanks for stopping by. Have a great day!

The Life and Times (and Fractions) of Eliza Acton

Title Page

You may know Eliza Acton as an English poet or Victorian cookbook author, but I prefer to think of her as the Queen of MP.6.

CCSS.Math.Practice.MP6:
Attend to precision.

Her bestselling Modern Cookery for Private Families — which was first published in 1845, ran through 13 editions by 1853, remained in print until 1918, was reissued in 1968 and 1974, and then resurrected again in 1996 by Southover Press, with two more editions since — might very well be the greatest cookbook ever produced.

The prose within the volume is magnificent. She included recipes for “Poor Author’s Pudding,” “Printer’s Pudding,” and “Publisher’s Pudding,” the last of which “can’t be made too rich.” The directions for the “Publisher’s Pudding” explain that it should be covered with a “sheet of buttered writing paper,” which no doubt gives recipe readers some idea about the thickness of paper to be used, but also implies something about the publishing industry. (The complete text is available from Google Books, if you’d like to check it out for yourself.)

But what makes this work mathematically interesting is that it is the first cookbook that used precise measurements in its recipes. Without Modern Cookery, a middle school word problem might look like this:

The recipe for a loaf of bread calls for some flour, a dash of salt, and enough water to make the dough pliable. How much salt would you need to make two loaves?

I suppose the answer is “two dashes,” though printers would likely call that an em dash. (Cue cheeky, all-knowing editor’s laugh here.)

It was the recipes of Ms. Acton — like the one for a disgusting drink known as Milk Lemonade, which calls for 6 oz. sugar, ¼ pint lemon juice, ¼ pint sherry, and ¾ pint cold milk — that paved the way for the wonderful word problems that students enjoy today:

My recipe calls for ⅔ cups of white flour and 2⅕ cups of wheat flour. How much flour do I need in total for my recipe?

Oh, wait… did I say wonderful? I meant awful.

Who the hell measures flour in fifths of a cup? And why would anyone need to know the total amount of flour? Just dump it in a bowl and mix!

The word problem above without specific measurements is purely speculative; it’s almost certain that someone else would have thought to include exact measurements had Eliza Acton not come along, and students would have still been subjected to unrealistic fraction-containing word problems. But the purported imprecision within recipes is spot on, as shown by this recipe taken from an early 18th century English text:

Fill yr pott halph full of wien & [a] good share of sugar. Milke in as much cream & stirr itt once about very softly. Let itt stand two houres before you eate itt.
[from MS Codex 753, compliments of rarecooking.com]

Admittedly, that recipe is for an Ordinary Sillibub, which is basically a red wine float, and hence the recipe is very nearly useless. But it is typical of the imprecision that was commonplace before Ms. Acton’s arrival.

All hail Eliza Acton, Queen of MP.6!

Fractional Eggs

I search for new recipes at allrecipes.com all the time. This morning, a search yielded a delicious recipe for pumpkin pancakes, which sounded like the perfect breakfast for a crisp fall morning.

One of the things I love about allrecipes is the ability to customize the number of servings. The default number of servings for the pumpkin pancake recipe was six, but I could adjust it to four, a more appropriate number for our two-adult, two-child family:

So I did. And as you’d expect, each item in the ingredient list was reduced to ⅔ its previous amount. Sort of. Two cups of flour was reduced to 1⅓ cups. One cup of pumpkin puree was reduced to ⅔ cup. But 2 teaspoons of baking powder was reduced to 1¼ teaspoons, and 1 teaspoon of cinnamon was reduced to ¾ teaspoon.

The reduction in the number of servings was 33⅓%, yet the range of reductions in the ingredients varied from 25% for salt (from 1 teaspoon to ¾ teaspoon) to 50% for ground ginger (from ½ teaspoon to ¼ teaspoon).

But I get it. It’s not typical for most kitchens to contain a spoon that measures ⅙ teaspoon. So there’s clearly some part of the algorithm that completes the conversion but then finds a “nice” fraction that’s in the right neighborhood. Fair enough.

But what the hell’s going on here?

Is it really better to display ⅝ egg instead of ⅔ egg? Couldn’t the algorithm recognize that fractional eggs just aren’t all that common and leave it as a whole number?

My guess is that the programmer is one of the folks to which this statement alludes:

5 out of 4 people aren’t very good with fractions.

That joke represents one-fifth of my favorite fraction jokes. Here are the other four:

Why won’t fractions marry decimals?
They don’t want to convert.

I’m right 4/5 of the time. Who cares about the other 10%?

There’s a fine line between a numerator and a denominator.

Sex is like fractions. It’s improper for the larger one to be on top.

If you find a store that sells ⅝ egg, please let us know about it in the comments.

Are Fractions Useless, or Are Americans Just Stupid?

I don’t know how else to say it, so I’m just gonna say it.

Fractions are full of sh*t.

Okay, not really. But if I have to hear one more time about how fractions are useful because of applications to cooking, I may commit harakari.

Before I jump into a diatribe, though, I absolutely have to share this improper fraction cartoon, which I believe was originally from Fat Rooster Studios (warning: rated PG-13).

It’s really hard to continue after that. But I’m gonna try.

There are three reasons that fractions are not really important in cooking.

• First, fractions only appear important because Americans are stupid. We insist on using the imperial system, and we measure dry ingredients in fractional parts of a cup. In other parts of the world, they don’t add 1 3/4 cups of flour to their recipe for croissants. Instead, they use 450 ml of flour. So making a half, a third, or a double recipe doesn’t involve operations with fractions.
• Second, ratios are important when cooking, not fractions. The exact amount of flour, sugar and baking powder in your chocolate chip cookies isn’t critical, so long as the ratio is 96 : 48 : 1. Approximately. Cooking is not an exact science. If your ratio of flour : sugar : baking powder = 98 : 45 : 2, you should still end up with a tasty dessert.
• Third — and, in my opinion, most importantly — great cooking derives from experience and approximation, not from exact measurements. My mother used to drive me crazy when she’d state, “But I followed the recipe,” if her normally fantastic lasagna came out less than fantastic.

Don’t believe me? Then watch the chef on a cattle drive as he makes chili over an open fire, and notice how he throws in a bucket of beans, two buckets of tomato sauce, and as much ground beef as he thinks is appropriate. You can bet your ass that Cookie ain’t got no measuring cups in the back of the chuck wagon. Or better yet, watch him make a cup of “six shooter coffee,” where his recipe is one handful of ground beans per cup of water. How much coffee is in a handful? Depends on the hand.

Maybe you think it’s just cowboys who estimate. Nope. Watch Emeril Lagasse as he adds a pinch of this, a dash of that, and — BAM! — the result is a grilled pork chop for which tourists pay $30 when they visit New Orleans.

If you need proof that ratios are the key mathematical element to successful cooking, listen to Dr. Mark Hadley. He claims that perfect ravioli is obtained when the ratio of pasta : filling : sauce = 45 : 45 : 10, which includes just enough olive oil “to give a thin layer of 200 microns over the surface of all the pasta – enough to make it glisten, resulting in the perfect mouthful.”

But, you know what? We shouldn’t let reality get in the way of a good story. Let’s please continue to perpetuate the myth that fractions are important — nay, critical — by including exorbitant numbers of cooking problems in the fraction units of textbooks. As far as I can surmise, the majority of fraction problem authors have never actually cooked. Here’s a typical problem:

The following recipe for Blueberry Bubble Loaf makes 12 servings.

• 2 cups cereal that contains blueberries
• 1 cup brown sugar
• 1/2 cup butter
• 2 packages of refrigerated buttermilk biscuits

Rewrite the recipe so that it makes 4 servings.

Let’s assume that this isn’t stupid. (Though it is, right? I mean, it might be reasonable to make 6 servings, since that would require just one package of refrigerated buttermilk biscuits. But to make just 4 servings? That means you’ll only need 2/3 package of refrigerated biscuits. What are you supposed to do with the other 1/3 of the package?)

But as presented, the solution requires that each ingredient be divided by 3. That gives 2/3 cup cereal, 1/3 cup brown sugar, 1/6 cup butter, and the aforementioned 2/3 package of refrigerated buttermilk biscuits. I decided to make this recipe.

• I have a 1/3-cup measure in my cooking drawer, so the first two ingredients were no problem.
• I don’t have a 1/6-cup measure. I could have measured 1/3 cup of butter and used an educated guess to divide the amount in half. Instead, I can just filled a 1/4-cup measure, and decided that that was close enough. Good enough for government work.
• I’ll only need 6 2/3 of the 10 biscuits that come in a 12-ounce container of refrigerated buttermilk biscuits. WTF? I decided that 7 biscuits is close enough, and I gave 3 uncooked biscuits to my dog. He’s happy at this development. I hope he doesn’t get worms.

I cooked the blueberry bubble loaf as directed, and it came out fine. Except that the total mixture only filled 1/3 of a bread pan, and it created a loaf that was only one inch tall. That’s not a loaf; that’s a tortilla.

But generally speaking, there was no material difference between the original loaf and my reduced-height loaf, despite the imprecision in my measurements. And do you know why there was no difference?

Because fractions are full of sh*t.

Now check this out. The following is a cake recipe from About.com.

• 2 cups cake flour
• 2 teaspoons baking powder
• 1/2 teaspoon salt
• 1/2 cup butter, softened
• 1 cup sugar
• 3 large eggs
• 2 teaspoons vanilla
• 3/4 cup milk

And here’s a vanilla cake recipe from Country Living.

• 1 1/2 cups cake flour
• 1 1/2 teaspoons baking powder
• 1/4 teaspoon salt
• 1/2 cup butter, softened
• 1 cup sugar
• 2 large eggs
• 1/2 teaspoon vanilla
• 1/2 cup milk

The second recipe requires 3/4 as much flour as the first recipe. If fractions really mattered, then every ingredient in the second recipe should have an amount that is 3/4 as much as the first recipe. But they don’t. There is 1/2 as much salt, the same amount of butter, the same amount of sugar, 2/3 as many eggs, 1/4 as much vanilla, and 2/3 as much milk.

So I’ll say it again.

Fractions are full of sh*t.

At least when it comes to cooking.

Fractions are, however, fodder for some great jokes.

Five out of four Americans have trouble with fractions.

Sex has a lot in common with fractions.
It’s improper for the larger one to be on top.

It’s hard to tell the difference between a numerator and a denominator. There is a fine line between them.

Two-thirds of Americans have trouble with fractions. The other half can handle them just fine.

Son: Can you help me find the lowest common denominator of 1/2 and 1/3?
Dad: You mean they still haven’t found it? They were looking for that when I was a kid!

7 Math Mistakes to be Aware Of

April is Math Awareness Month, and some things to be aware of this month — as well as the whole year through — are common math errors. Here are seven that show up frequently.

Incorrect Addition of Fractions. It’s common for kids to add fractions as follows:

And while that algorithm works for batting averages in baseball, it doesn’t work in most other places. More importantly, this mistake is often unaccompanied by reasoning. For example, a student who claims that 2/3 + 4/5 = 7/9 doesn’t realize that with each addend greater than 1/2, then the sum should be greater than 1. That lack of thought bothers me.

Cancellation of Digits, Not Factors. While it’s true that 16/64 = 1/4 and 19/95 = 1/5, students who think the algorithm involves cancelling digits may also argue that 13/39 = 1/9, and that just ain’t right.

Incorrect Distribution. This one takes a lot of forms. In middle school, kids will say that 4(2 + 3) = 8 + 3. As they get older, they apply the distributive property to exponents and claim that (3 + 4)² = 3² + 4² or, more generally, that (a + b)² = a² + b².

The Retail Law of Close Numbers. A large portion of the population will buy a shirt for $19.99 that they’d pass up if it had a price tag of $20.00. Even though the amounts only differ by one cent, a lesser digit in the tens place makes the price feel much lower. Crazy, but true.

Ignoring the Big Picture. If you are a driver who is interested primarily in speed (and less concerned with price, looks, fuel efficiency, or other factors), would you rather have a vehicle with 305 horsepower or one with 470 horsepower? If you chose the latter option, congratulations! While the owner of a sweet 305-hp Ford Mustang will be sitting at home and sipping a mint julep on his front porch, you’ll still be doing 30 mph on the highway in your Sherman tank.

Correlation Implies Causation. As ice cream sales increase, the number of drowning deaths increases, too. But that doesn’t mean that having an ice cream cone willl make you less likely to swim safely, even if you failed to heed your mother’s advice to wait 30 minutes after eating. It’s just that ice cream sales and swimming-related deaths increase in summer, both of which are to be expected.

Just because two things happen to coincide doesn’t mean that one is the direct (or even indirect) result of the other.

Percents Don’t Work That Way. A 20% decrease followed by a 20% increase does not return you to the initial value. If you invest $100 in a company, and it loses 20% the first year, your investment will then be worth $80. If it gains 20% the next year, you’ll now have $96. Uh-oh.

What common math error do you see frequently, and which one bothers you the most?

The Twelve Days of Crisp Math – Day 4

Did you know that five out of four people have trouble with fractions? Hopefully you won’t have any trouble with this joke on the Fourth Day of Crisp Math…

What did the dollar say to four quarters?
You’ve changed!

Football Math for Super Bowl Week

Super Bowl week seems an appropriate time to share some jokes that involve football and math.

[Super Bowl Squares Online Contest]

What is this?

B
BA
BACK

Here’s another one involving fractions. (And that lead-in should be a hint if you had trouble with the question above.)

What do you call a Patriots fan with half a brain?
Gifted!

And just to be an equal opportunity offender…

What did the average Giants player get on his Wonderlic test?
Drool.

There are several one-liners involving football and math (sort of).

Pro football players are so huge, it takes only four of them to make a dozen.

Their nickel defense is only worth 3¢.

His uniform number was 29, which was also his house number. He wore it to make sure he remembered where to go after the game.

That last one reminded me of a mathy football joke involving dumb people…

By the time Bubba arrived to the football game, the first quarter was almost over. “Why are you so late?” his friend asked.

“I tossed a coin to decide between going to church or coming to the game.”

“I don’t understand. How long could that have taken?”

“Well,” Bubba said, “I had to toss it 14 times.”

For a similar, non-football coin-tossing joke, read the one about the student at the final exam.