Change the Vowel

The following puzzle contains a clue within each clue. The answer, of course, fits the clue, but each answer is also one of the words within the clue with its vowel sound changed. For instance, the clue “the distance from the top of your hat to the sole of your shoes” contains the word hat, and if you change the vowel sound from a short a to a long i, you get height, which fits the description.

As always, there’s a catch. Every answer to the clues below is a mathy word.

1. The number of permutations of three different colored socks.
   
2. This value is the same for 3 + 1 and 2 + 2.
3. Do this with two odd numbers and you’ll get an even number.
4. Three hours before noon.
5. You may fail to correctly expand (a + b)(c + d) if you don’t remember this mnemonic.
6. One represents this fractional portion of toes on the hoof of a deer.
7. The last element of a data set arranged in descending order.
8. The measure of central tendency made from the most common data points.
9. The number of contestants ahead of third place if there’s a tie for first place.
10. If the leader is forced to drop out of a race, the runner-up takes over this place.
11. The square root is needed to calculate the length of the hypotenuse in this type of triangle.
12. The graph of the declination of the Sun during a year can be approximated by this type of curve.

Answers

1. six
   
2. sum
3. add
4. nine
5. FOIL
6. half
7. least
8. mode
9. two
10. first
11. right
12. sine

Constant Change

I’m frustrated.

I’m also old, cranky, and cynical. Whatever.

My frustration is not the my-flight-was-delayed-three-times-then-eventually-cancelled-and-there-are-no-more-flights-to-Cleveland-till-tomorrow-morning type. It’s not even the can’t-believe-my-boss-is-making-me-go-to-Cleveland kind of frustration. More like the why-aren’t-there-the-same-number-of-hot-dogs-and-buns-in-a-pack variety. So it’s a First World problem, to be sure, but still annoying. I’ll explain more in a moment.

But first, how ’bout a math problem to get us started?

If you make a purchase and pay with cash, what’s the probability that you’ll receive a nickel as part of your change?

Sure, if you want to get all crazy about this, then we can take all the fun out of this problem by stating the following assumptions:

• You only pay with paper currency. If you paid with coins, then the distribution of coins you’d receive as change would likely vary quite a bit.
• You never use 50¢ coins. Honestly, they’re just too obscure.
• Transaction amounts are uniformly distributed, so that you’re just as likely to receive 21¢ as 78¢ or any other amount.
• Cashiers don’t round because they dislike pennies. So, if you’re supposed to get 99¢ change, the cashier doesn’t hand you a dollar and say, “Don’t worry about it.” Instead, you actually get 99¢ change.

But stating assumptions is a form of mathematical douchebaggery, isn’t it? (As an aside, check out the definition of douchey that’s returned when you do a search. Sexist, anyone?) I prefer problems with no assumptions stated; let folks make their own assumptions to devise a model. If you and I get different answers because of different assumptions, no worries. Maybe we both learn something in the process.

Anyway, where was I? Oh, yeah…

Understanding the solution to that problem is a precursor to the issue that’s causing me frustration. I’ll give the solution in a minute, so pause here if you want to solve it on your own, but let me now allow the proverbial cat out of its bag and tell you why I’m frustrated.

At our local grocery store, there’s a coin counting machine that will count your change, sort it, and spit out a receipt that you can take to the customer service desk to exchange for paper currency. Walk in with a jar full of change, walk out with a fistful of fifties. Pretty nifty, right? Except the machine charges a ridiculous 8.9% fee to perform this service. No, thank you.

My bank used to have a similar coin counting machine, and if you deposited the amount counted by the machine into your account, there was no fee. The problem is that everyone was doing this to avoid the grocery store fee, so the machine broke often. The bank finally decided the machine wasn’t worth the maintenance fees and got rid of it. Strike two.

Which brings me to my current dilemma. One Saturday morning every month, we now spend 30 minutes counting coins and allocating them to appropriate wrappers. Which is fine. The problem, however, is that we run out of quarter and penny wrappers way faster than we run out of nickel or dime wrappers. Which brings me to the real question for the day:

Since pennies, nickels, dimes, and quarters are not uniformly distributed as change, why the hell does every package of coin wrappers contain the same number for each coin type?

The Royal Sovereign Assorted Coin Preformed Wrappers is the best-selling collection of coin wrappers on Amazon, and it provides 54 wrappers for each coin type. They also offer a 360‑pack with 90 wrappers for each coin type; Minitube offers a 100‑pack with 25 wrappers for each coin type; and Coin-Tainer offers a 36‑pack with 9 wrappers for each coin type. But what no one offers, so far as I can tell, is a collection of coin wrappers with a distribution that more closely resembles the distribution of coins that are received as change.

Whew! It feels good to finally raise this issue for public consideration.

So, the question that I really wanted to ask you…

Given the distribution of quarters, dimes, nickels, and pennies that are received in change, and given the number of coins needed to fill a coin wrapper — 40 quarters, 50 dimes, 40 nickels, and 50 pennies — how many of each wrapper should be sold in a bundled collection?

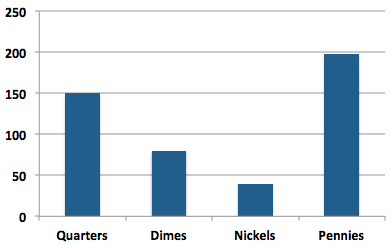
To answer this question, I determined the number of coins of each type required for every amount of change from 1¢ to 99¢. The totals yield the following graph:

The number of pennies is nearly five times the number of nickels. And there are nearly twice as many quarters as dimes.

But I realize that’s a theoretical result that may not match what happens in practice, since this assumes that the amounts of change from 1¢ to 99¢ are uniformly distributed (they aren’t) and that cashiers don’t round down to avoid dealing with pennies (they do). In fact, when I made a purchase of $2.59 yesterday, instead of getting one penny, one nickel, one dime, and one quarter as change, the cashier gave me one penny, three nickels, and one quarter, in what was clearly a blatant attempt to skew my data.

So for an experimental result, I counted the pennies, nickels, dimes, and quarters in our home change jar. The results were similar:

The ratio of pennies to nickels is closer to three, but the ratio of quarters to dimes is still roughly two.

Using a hybrid of the theoretical and experimental results, and accounting for the fact that only 40 quarters and nickels are needed to fill a wrapper whereas 50 pennies and dimes are needed, it seems that an appropriate ratio of coin wrappers would be:

quarters : dimes : nickels : pennies :: 17 : 8 : 6 : 19

Okay, admittedly, that’s a weird ratio. Maybe something like 3:2:1:4, to keep it simple. Or even 2:1:1:2. All I know is that 1:1:1:1 is completely insane, and this nonsense has got to stop.

Hello, Royal Sovereign, Minitube, and Coin-Tainer? Are you listening? I’ve completed this analysis for you, free of charge. Now do the right thing, and adjust the ratio of coin wrappers in a package accordingly. Thank you.

---

Wow, that was a long rant. Sorry. If you’ve made it this far, you deserve some comic relief.

How many mathematicians does it take to change a light bulb?
Just one. She gives it to a physicist, thus reducing it to a previously solved problem.

If you do not change direction, you may end up where you are heading. – Lao Tzu

The only thing that is constant is change. – Heraclitus

Turn and face the strange ch-ch-ch-changes. – David Bowie

A Buddhist monk walks into a Zen pizza parlor and says, “Make me one with everything.” The owner obliged, and when the pizza was delivered, the monk paid with a $20 bill. The owner put the money in his pocket and began to walk away. “Hey, where’s my change?” asked the monk. “Sorry,” said the owner, “change must come from within.”

---

As for the “probability of a nickel” problem that started this post, here’s my solution.

For change amounts from 1¢ to 25¢, there are ten values (5‑9 and 15‑19) for which you’ll receive a nickel as part of your change.

This pattern then repeats, such that for change amounts from 25n + 1 to 25n + 25, where n is the number of quarters to be returned, you’ll receive a nickel when the amount of change is 25n + k, where k ∈ {5, 6, 7, 8, 9, 15, 16, 17, 18, 19}. For 0 ≤ n < 4, there are 40 different amounts of change that will contain a nickel, so the probability of getting a nickel as part of your change is 40/100, or 40%.

Teasing Out Some Math Jokes

Let’s do a quick warm-up before jumping into this post.

A boy leaves his house headed for school, walking at a rate of 4 miles per hour. Ten minutes later, his sister leaves the school headed for home, walking at a rate of 3 miles per hour. Assuming they travel the same route (just in opposite directions), which one will be nearer the school when they meet?

This problem is based on the first puzzle that appears in Mathematical Teasers by Julio A. Mira. As best I can tell, this book is out of print, and probably for good reason. Written in 1970, it contains no semblance of political correctness. For instance, the image below appears at the beginning of Chapter 1:

Click to Enlarge Image

Hmm… a pigtailed coed in a skirt sitting on a desk, tickling the chin of a math professor? There is no doubt an editor in 2013 would prohibit such an image from appearing in a publication; quite honestly, I’m even surprised an editor allowed it 43 years ago.

My copy of this book was obtained when the National Council of Teachers of Mathematics cleaned out their staff library. Inside the front cover, an insert states that it was a review copy “sent with the compliments of Barnes and Noble, Inc.,” and a stamp on the insert reads:

RECEIVED
MAY 26 1970
NCTM

Despite its political incorrectness and outdated contexts, my five-year-old sons have been enjoying the puzzles in the book. But they aren’t just puzzles. Like the warm-up problem above, they are jokes, in the sense that the punch line (answer) is unexpected. The following are a few of my favorites.

1. A man with $50 in a bank account withdraws $20, leaving $30. He then withdraws $15, leaving $15. Then $9, leaving $6. And finally $6, leaving $0. The sum of his withdrawals is 20 + 15 + 9 + 6 = $50, as expected, but the sum of the remainders is 30 + 15 + 6 + 0 = $51. Where did the extra dollar come from?
2. If it takes 3 minutes to boil an egg, how long will take to boil a dozen eggs?
3. How many cubic inches of dirt are in a hole that measures 1 ft. × 1 ft. × 1 ft.?
4. A man purchased a pair of shoes that cost $25 and gave the shop owner a $100 bill. After the man left with the shoes and his change, the owner took the $100 bill to the bank, where he was told that it was counterfeit. What was the total loss to the owner?
5. Every day, Johnson’s cat would climb 11 feet higher in a tree that is 63 feet tall. But every night, the cat would climb back down 7 feet. How many days would it take her to reach the top of the tree?

No answers will be posted. Y’all can attempt to reach consensus in the Comments section.

The Twelve Days of Crisp Math – Day 4

Did you know that five out of four people have trouble with fractions? Hopefully you won’t have any trouble with this joke on the Fourth Day of Crisp Math…

What did the dollar say to four quarters?
You’ve changed!

Career Changes

When I give math joke presentations, I bombard the audience with several groan‑inducing puns. When they can take no more, I admit to them that (a) stand‑up comedy is NOT my full-time job and (b) I am not considering a career change. This admission usually provokes a collective sigh of relief from the audience.

I inform them, however, that I have several friends who recently changed careers.

I have a friend who used to be a statistician.
Now she’s a gynecologist.
Her specialty is histerectograms.

I have a friend who used to be a combinatorist.
Now she is a hairdresser.
She works with combs and perms.

I have a friend who used to be a high school math teacher.
Now he’s a densist.
He performs square root canals.

I have a friend who used to be a geometer.
Now he’s a taxidermist.
His specialty is Fourier (furrier) transforms.

I know a former inmate.
He became a poet.
Now he writes converse.

I have a friend who used to be a transformational geometer.
Now he polishes mirrors.
He specializes in reflections.

As you might well imagine, telling an audience about these career‑changing friends usually elicits more groans. Go figure.

I particularly like this joke format, so I’ll offer a challenge to you: Create a joke about a career-changing professional. Feel free to use the form below, use this Google Docs form, or place your joke in the Comments.

Retail Tales

In tough economic times, lots of folks are counting quarters and pinching pennies. To attract new customers, retailers are offering significant discounts.

• A local bookstore is having a sale: All Math Titles, 1/3 Off. So I picked up a copy of Gödel, Escher.
• Skate Charm Insurance is offering fire-and-theft policies at rock-bottom prices. When asked how they could offer them so cheap, the actuaries responded, “Who would steal a burnt car?”
• Grocery stores in Northern Virginia are promoting lite beer as a good deal, because it has 20% fewer letters than light beer.
• A local gas station recently switched to metric, and I somehow feel better paying $1 per liter instead of $3.78 per gallon.

Nobody likes change, except a kid with a piggy bank.

What coin doubles in value when half is removed?
A half dollar.

Doc: Give me an update on the boy who swallowed four quarters.
Nurse: No change yet.

In the shameless plug department: NCTM members get a 25% discount off the retail price of Math Jokes 4 Mathy Folks at NCTM conferences, and everyone else can save 24% by buying from Amazon.

Was Darrell Huff at the State of the Union Address?

Perhaps my all-time favorite joke:

How many school administrators does it take to change a light bulb?
Cha-a-a-a-a-a-a-a-ange?

Or, if you prefer:

How many school administrators does it take to change a light bulb?
What was wrong with the old light bulb?

These jokes seem particularly relevant after listening to last night’s State of the Union address. Here’s why.

President Obama made a bold statement about his plans for the future of education. “Over the next ten years, with so many Baby Boomers retiring from our classrooms, we want to prepare 100,000 new teachers in the fields of science, technology, engineering and math.”

Oh, please. I’m a Steel Town Democrat and generally an Obama supporter, but this is another instance of using a big number to sound impressive. Bill Clinton employed a similar tactic in his 1998 State of the Union address, when he announced funding for the training of 100,000 additional teachers to help reduce class size. Truth is, adding 100,000 teachers to the current pool of 3,000,000 teachers would only reduce class size by about 3% — which translates to 1 pupil fewer in a 25‑student classroom.

The problem is, 100,000 just isn’t enough. In 2007, Barbara Pytel claimed that hundreds of thousands will leave the teaching profession in the next few years as the baby boomer generation enters retirement. Her prediction for math and science was particularly dire. “It is estimated that the US will have a shortage of 280,000 math and science teachers by 2015” (Baby Boomer Teachers Retiring: Study Predicts Major Problem by 2015).

So what good will only 100,000 new teachers do? That’ll still leave a shortfall of 180,000.

In March 2009, Richard Ingersoll and David Perda of the University of Pennsylvania calculated that colleges and universities actually produce 150% more math and science teachers than schools require to replace those who are retiring. That’s right. Annually, the number of new teachers is 2.5 times the number that leave due to retirement.

The problem isn’t the number of new teachers or the number who retire. It’s the number of teachers who leave the profession for a better job. Statistics vary wildly, but some estimates say that 1/3 of new teachers leave the profession within 3 years, and up to 1/2 leave within 5 years.

Why do teachers leave? We all know the answers, and we have data to prove it. In the study by Ingersoll and Perda, they found that 59.9% of teachers said they leave the math classroom because of poor salary and benefits, and 67.5% said they leave because there was inadequate time to plan and prepare. Really? You mean teachers want time to do a good job, and they want to be adequately compensated for their efforts? Go figure.

Last night President Obama said, “In South Korea, teachers are known as ‘nation builders.’ Here in America, it’s time we treat the people who educate our children with the same kind of respect.” Yeah, no kidding. If you really believe that teachers deserve more respect, then please stop trying to deceive us with large numbers, Mr. President. Instead, how about some effort toward improving the salary and working conditions for our nation builders?

In his defense, I believe Obama is willing to take the steps necessary to resuscitate a broken system. Last night, I just kept wishing that he would have talked about his plans for reform that might actually fix the problem.

BONUS: Speaking of using large numbers to deceive, here’s a math problem for you. A radio commercial several years ago attempted to promote the selectivity of Dunkin Donuts. The commercial stated, “We reject more than 1,000,000 pounds of coffee beans a year.” Are they really that picky? Do a quick, back-of-the-envelope calculation to determine the percent that they reject. You can find information online about the number of Dunkin Donuts stores in the world, the amount of beans needed to make a cup of coffee, how many cups are sold, and so on. And even if you can’t, make some conservative estimates. You’ll still be surprised by the answer your calculation reveals.