Archive for March, 2013
Bedtime Math
You’ve probably heard of Read 20, a movement where parents are encouraged to read with their children at least 20 minutes a day. But Bon Crowder thinks that this shortchanges math, so she started an initiative that she calls Count 10, Read 10. While I dislike the name — math is so much more than counting — I love the sentiment.
My sons are regularly exposed to more than 10 minutes of math during daylight hours, but I’m still happy to give them another 10 minutes of math right before bed. Sometimes we use the material from Bedtime Math, but I hate the traditional problems that they serve up. I prefer instead to create new, original problems that are a bit more interesting.
This is a double-edged sword.
My kids love the problems I create, but now they’ve come to expect a new problem daily. So every night while they’re brushing their teeth, I’m mentally preparing a bedtime math lesson plan.
This has caused a lot of angst. I’m just not that creative. But two evenings ago, I crafted a problem worth sharing.
Like most five-year-olds, my kids are infatuated with the seasons. They know that the vernal equinox is usually on March 21 (they forgot, and so did I, that it’s on March 20 in 2013), they know that there is an equal amount of daylight and darkness on the equinox, and they also know that the days will continue to get longer until the summer solstice. [update – Thanks to Caitlin for the reminder about the equinox in 2013.] I asked a few questions about these facts to prime the pump, then I posed this question:
What is the difference between the number of minutes of daylight and the number of minutes of darkness today?
Alex speculated that there are two minutes more of daylight every day, so he guessed that there would be 14 more minutes of daylight. Eli made a wild-ass guess and thought it would be closer to an hour.
This led to a great discussion. If there are 12 hours of daylight on March 21 and there are approximately 15 hours of daylight on June 21 (in northern Virginia, anyway), and assuming a linear increase, then approximately 3 hours ÷ 90 days = 2 minutes of daylight are added each day. So the estimate of 14 minutes was actually pretty accurate.
As it turns out, the vernal equinox doesn’t really have an equal number of hours of daylight and darkness. There were exactly 12 hours of daylight on March 17, and there were 12 hours, 10 minutes of daylight on March 21. On March 28, there were 12 hours, 28 minutes, so the difference between that day and March 21 was actually 18 minutes.
But who cares?
The math discussion we had as a result of this question lasted at least ten minutes, so we met the goals of Count 10, Read 10. But as I said above, my kids get way more than ten minutes of math a day. Earlier today, they amused themselves for half an hour with the following problem:
Start at the 1 in the lower left corner. With each move, proceed up or to the right (never left or down). As you move, perform the operations. What path will give the maximum value when you reach the 1 in the upper right corner?
Hopefully, you’ll be able to solve this problem in less than 10 minutes before you go to bed tonight. Good luck!
Math Jokes for Easter — Who Knew?
 Today is Holy Thursday, which my mother always used to call Maundy Thursday. Yet she could never tell me what Maundy meant. (In her defense, Google didn’t exist back then.) Maundy refers to the ceremony of washing the feet of the poor, especially in commemoration of Jesus washing His disciples’ feet on the day before the Last Supper.
Today is Holy Thursday, which my mother always used to call Maundy Thursday. Yet she could never tell me what Maundy meant. (In her defense, Google didn’t exist back then.) Maundy refers to the ceremony of washing the feet of the poor, especially in commemoration of Jesus washing His disciples’ feet on the day before the Last Supper.
This, of course, is only relevant to Christians. But since there are over two billion Christians on the planet, and since I pander to large groups, here are some math jokes to get all of us ready for Easter.
Rome is lousy with the papalcy.
In Vatican City alone, there are two popes per square kilometer.Some say the pope is the greatest cardinal. But others insist this cannot be so, as every pope has a successor.
Which is better, eternal bliss or a ham sandwich?
The ham sandwich, of course. Nothing is better than eternal bliss, and a ham sandwich is better than nothing; therefore, a ham sandwich is better than eternal bliss.
And finally…
A great logician (some say it was Betrand Russell; others say it was Andrew North Whitehead) once claimed that he could prove anything if it is assumed that 1 + 1 = 1. An audience member then asked, “Can you prove that you’re the Pope?” He thought for a moment and then proclaimed, “I am one. The Pope is one. Therefore, the Pope and I are one.”
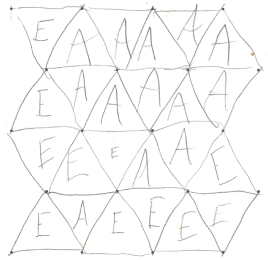
Using Dynamic Paper to Make Math Game Boards
While exploring hexagon patterns last night, Eli suggested, “Let’s play Dots and Boxes using hexagons instead of squares.” Well, now, that’s an inspired idea! So I used the Dynamic Paper tool from Illuminations to create isometric dot paper. The boys then played Dots and Triangles, actually — hexagons would work, but you’d have to remove some of the dots — and Alex narrowly edged Eli.
I am continually blown away by the power of Dynamic Paper. Suggested by a participant at the 2009 Illuminations Summer Institute and built by Math Resources, this tool does it all —
- Need the net of an icosahedron whose sides are exactly 0.58 inches? Yep, Dynamic Paper can do that. And it’ll generate a printable 8.5″ × 11″ PDF of the net that you can cut out, fold up, and tape together.
- Need graph paper with trig coordinates, going from ‑2π to 2π on the x-axis, with axis tick marks starting at ‑π and appearing every 2π/3 units? Well, sure, it’ll look crazy as hell… but if that’s what you want, Dynamic Paper aims to please.
- Need a tessellation of hexagons? It can do that, too, but first you have to decide if you want a Type I, Type II, or Type III tessellation. What’s that, you didn’t know there were three different types of hexagon tessellations? No worries. Dynamic Paper can make all three types, and it won’t even stick out its tongue at you while it creates them.
It also does attribute blocks, spinners, number lines, isometric dot paper, and a million other things. But I don’t have the time to list them all. Just go check it out.
The following are instructions for five different math games you can play, using game boards that you can create with Dynamic Paper.
Dots and Triangles. Go to Graph Paper → Isometric Dot Paper. Pick the number of rows, columns, and distance between dots, then click Add. Press Download PDF, and print it. The game is played with players connecting two dots with a straight line. If a player draws a line that forms a small equilateral triangle, that players puts her initial (or some other distinguishing mark) inside the triangle to claim it. In general, players alternate turns, but if you make a line that completes a triangle, you get another turn, which can often lead to four, five, six, or more triangles being created by a player on one turn. See the rules for Dots and Boxes for more information.
Hex. Go to Tessellations → Build Your Own → Hexagons (Type I, II or III). Make the tessellation as wild as you like, then click Add. Adjust the tessellation so that there are the same number of hexagons vertically and horizontally. Then play Hex, with one player trying to form an unbroken line of hexagons from top to bottom, and the other trying to form an unbroken line of hexagons from one side to the other. (Decide who’s trying for a vertical or horizontal line before play begins.) Players then alternately choose one of the hexagons and claim it by placing an initial in the hexagon. First one to form an unbroken line wins.
- Sample Hex Game Board (PDF)
Note: This board is 8 hexagons tall but only 7 hexagons wide, so the player trying to connect top to bottom should go first.
Make 12. Go to Graph Paper → Grid Paper, choose the number of rows and columns, and then enter the same value for the row height and column width. Players then alternately create rectangles with an area of 12 square units. The last player to place a rectangle wins. For variations, use a different size rectangle, or play that the last player to place a rectangle loses.
Secret Number. Okay, you don’t really need a board game for this one, but a board can be useful to keep track of numbers that have been eliminated. With Dynamic Paper, go to Number Grids, and you can make a grid of numbers from m to n, where m and n can have any values you like. For young kids, I use a hundreds board, but why not try a grid with numbers from 38 to 73 with six numbers in each column? To play, one player secretly chooses a number, then the other player(s) ask questions such as, “Is the number odd or even?”, “Is the units digit a 5?” or any other yes-no question. The only yes-no question not allowed is, “Is __ your number?”
Polar Coordinate Battleship. Just like regular battleship, but for older kids. Go to Graph Paper → Polar Coordinates, then set your parameters. Have each player place one ship each of length 2, 3, 4, and 5 units. (Some people allow ships to be placed on a curve. I think that’s unacceptable except for the 2‑unit ship, but you can play however you like.)
What math games do you play? Can Dynamic Paper be used to create the game boards for any of your favorite math games?
Mathy Birthday Problems
Last week, I turned 42. Here’s a math problem related to that number.
Take 27 cubes, numbered consecutively from 1 to 27. Arrange them into a magic cube so that every row, column, corridor, and space diagonal has a sum of 42.
If that’s too much for ya, try this problem instead. It’s a slight modification of a math problem that appeared on the birthday card given to me by colleagues.
Two men my age go out for drinks at 10 o’clock on a Saturday night. One of them drinks six 12-ounce beers, each of which is 8% ABV. The other drinks four Lynchburg lemonades, each of which contains one ounce of 80-proof Jack Daniels and one ounce of 60-proof triple sec. Assuming the men are the same size, which one gets more drunk?
The answer to the first question can be found at Math Palette.
The answer to the second one? Trick question. Men my age don’t go out after 10 o’clock.
Math of the Irish
My friend and I were enjoying a pint of Guinness at a local Irish bar. The following sign hung overhead.

While enjoying the pint, another patron came up to me. “Quick!” he said. “Gimme a number!”
“What?” I asked.
“Gimme a number!” he repeated.
“Okay… 27?”
“27 × 2 = 54,” he said. He then turned to my friend. “Now you give me a number!” he demanded.
“Uh, 19,” my friend offered.
“19 × 2 = 38.”
He then made his way from table to table, each time asking for a number, then multiplying it by two. After completing an entire lap around the bar, he returned to our table. “Gimme a number,” he asked me again.
“Dude,” I said. “What’s up with you? Why do you keep asking people for numbers, then multiplying by two?”
“What can I say?” he said. “I love Dublin!”
Happy St. Patrick’s Day!
Einstein > π
Yes, today is Pi Day.
Whatever.
More importantly, it’s the 134th anniversary of Albert Einstein’s birth. (Isn’t it remarkable that people who celebrate Pi Day don’t think to add a few candles to the pie and sing Happy Birthday to Big Al?) It’s interesting that 134 shares the same three digits as Einstein’s birth date, 3/14, and 134 also has the following property:
1 + 3 + 4 = 8
8C1 + 8C3 + 8C4 = 134
On his birthday, we can honor Einstein by remembering some of his quotes. One of his most famous is about his math ability.
Do not worry about your difficulties in mathematics. I can assure you that mine are still greater.
Slightly less well-known is the following quote by Einstein, also about math.
God does not care about our difficulty with numbers. He integrates empirically.
But special for today, the following is a quote not from Eistein, but about Einstein. The quote is attributed to a Japanese cartoonist, Ippei Okamoto, and appeared in Driving Mr. Albert by Michael Paterniti.
He [Einstein] has a quiet way of walking, as if he is afraid of alarming the truth and frightening it away.
A beautful quote for a beautiful mind. Happy Birthday, Mr. Albert!
Don’t Get Mad, Get Equal
The title of this post is a modification of a common idiom. It doesn’t make much sense, but if people are allowed to use even when they mean equal, then vice versa.
A math terminology debate over these two words occurred in our house yesterday.
While walking my dog, I found a shiny, new penny. When I got home, I told my sons that whoever guessed the item I found could have that item. To my dismay, my mother-in-law, father-in-law and wife started making suggestions. “Maybe it’s a penny,” my wife suggested. “Or a quarter,” said my mother-in-law. “Or a dime,” said my father-in-law. I looked at my dog. C’mon, boy, you’re the only one who hasn’t said anything. Why don’t you suggest that it could also be a nickel and make this game completely devoid of fun, I thought.
But kudos to Eli for what he did next. “Is it a coin?” he asked, and I could almost see his five-year-old brain thinking that this would make him a winner no matter which of the suggested coins it was.
“It sure is!” I said, beaming, and handed him the coin.
We play games like this all the time, and each of my sons wins in roughly equal proportions. But upon seeing Eli receive a penny, my mother-in-law must have sensed favoritism. She pulled out her coin purse and handed some coins to both boys. When the dust settled, Eli had two nickels and three pennies, but Alex had just one nickel and three pennies. Alex asked why he had received fewer. It was just an oversight, and Grandma gave him another nickel.
“Now we have an even number of coins,” Eli said.
“Actually, you have an equal number of coins,” I corrected. “Five isn’t an even number.”
“Oh, come on,” said my mother-in-law. “They’re five years old.”
“I’d rather them not use math words incorrectly,” I said. “You’d correct them if they called a firetruck an ambulance, wouldn’t you?”
“That’s different,” she said.
Only because you know the difference between a firetruck and an ambulance, but not between even and equal, I thought. But I didn’t say anything.
As it turns out, the Google dictionary lists equal as a synonym for even. In that case, however, equal means being in equilibrium or balanced, not having the same number or value, so there is a subtle distinction. Then again, the Google dictionary also gives regardless as the definition for irregardless, which isn’t even a word, and if it were, it should mean the opposite of regardless, right? The work of lexicographers often reflects how we speak and not how we ought to speak, so it won’t be long before equal and even have the same definitions.
What do you think? Are even and equal synonyms? Are there other math words that are used interchangeably but shouldn’t be?
My mother-in-law and I often have these little exchanges, but for the most part, we get along well. She is an exceptionally wonderful grandmother, she is generous and kind, and her penchant for dark beers makes her an instant friend. I love her dearly.
Yet these debates make me realize why other folks disparage their in-laws. If my mother-in-law and I had these debates and she weren’t otherwise wonderful, I might speak ill of her, too. And then I might make math mother-in-law jokes like the following:
I’ve got nothing against polygamy. I just don’t know how one man could tolerate that many mother-in-laws.
Or this one from comedian Les Dawson:
My mother-in-law caused an argument in a pub, and a half dozen men dragged her to the floor, screaming. The barman turned to me and asked, “Aren’t you going to help?”
“Nah!” I said. “Six should be plenty!”
Not long ago, I was told that I only had three months left to live. So my wife and I moved in with my mother-in-law, knowing it would feel a whole lot longer. One night, the three of us sat down for dinner, and my wife opened a bottle of wine. My wife read from the label, “Full-bodied and imposing, with a sharp bite and a bitter aftertaste.” She took a sip. “I think that’s a perfect description!” she said.
“Me, too,” I added. “But how does the winemaker know your mother?”
Hiring, Firing, and Flipping Coins
Tomorrow, I become the Director of Mathematics at Discovery Education, and I am slated to spend five hours with the Human Resources department, filling out paperwork and such. By the end of it, I suspect I’ll feel like Arlo Guthrie in Alice’s Restaurant:
…the sergeant came over, had some paper in his hand, held it up and said, “Kids, this piece of paper’s got 47 words, 37 sentences, 58 words, we wanna know [blah, blah, blah, blah],” and he talked for 45 minutes and nobody understood a word that he said, but we had fun filling out the forms and playing with the pencils…
I do not mean to disparage Discovery’s HR department, but my new boss has described this orientation as “a test of attrition.”
The following two days will be less bureaucratic but similarly intense. As I am the first employee hired for “the math team,” it will be my job to hire others, so my second and third days at Discovery will consist of six interviews with potential math specialists. Six! Hopefully it won’t go like this:
Three candidates are being considered for a job. The first candidate, a pure mathematician, steps into the interview room. The interviewer asks just one question, “What is 1/3 + 2/3?”
Without hesitation, the pure mathematician answers, “1.”
An applied mathematician enters next and is asked the same question. He takes out his calculator, punches some buttons, and announces, “0.99999999.”
Finally, a statistician enters the room and is asked the same question. “What is 1/3 + 2/3?” the interviewer asks.
The statistician responds, “That depends. What would you like it to be?”
My worry with so many back-to-back interviews is falling into the Gambler’s Fallacy. Just as a gambler incorrectly assumes that a string of successive heads must eventually be broken by tails, interviewers often believe that a string of successive weak candidates must eventually be broken by a strong candidate. In a recent interview with Steve Inskeep on NPR (Deciphering Hidden Biases During Interviews), Shankar Vedantam said…
…interviewers add the equivalent of two years of job experience to the last candidate in a row, who is weak, in order to break the streak.
Vedantam went on to say that Uri Simonsohn from the Wharton School of Business thinks interviewers should…
…have a spreadsheet where they can see all the candidates they’ve interviewed, not just on that one day, but over several days. And when you step back and actually say, “Yeah, there are an equal number of strong and weak candidates,” even though you may have the streaks of four or five really strong or really weak candidates in a row.
And who am I to argue with advice like that?
For you, I offer the Clusters spreadsheet, which can be used to simulate 100 coin tosses. Press F9 to generate a new set of tosses. The spreadsheet will then calculate the number of heads, the number of tails, and the longest run of either type. It shows that unexpected strings of consecutive heads and tails occur, but over the long run, the number of heads and tails are roughly equal, just as the number of strong and weak candidates who are being interviewed.
Just between you and me, though, I’m hoping for a slight imbalance toward the strong end.
Turn the Page
After eight fantastic years as the Online Projects Manager at NCTM, it’s time for my next chapter. On Monday, I become the Director of Mathematics for Discovery Education, leading a team that will build digital math techbooks for K‑12. I’m looking forward to building something great. As I mentioned during my interview, “I’m not coming to Discovery to create a textbook; I’m coming to create a movement.”
Leaving is such sweet sorrow. I’ll miss my friends and colleagues at NCTM, and I’m sad that I’ll no longer be creating resources for Illuminations. On the upside, my departure brought three stories worth sharing.
A Day Off
My last day at NCTM was February 28. That evening, I mentioned to my sons that I would not be going to work the next day. “Do you know why not?” I asked them. Alex suggested, “Because it’s Dr. Seuss’s birthday?” I love that! Celebrating the birth of Theodore Seuss Geisel certainly seems like a great reason for a federal holiday, but the truth is that I was just taking some time off between jobs.
Lesson Learned
The east coast was hit with a snowstorm during my time off, and both the NCTM and Discovery offices were closed. Had I been employed by either organization, I would have spent a day at home with pay. Instead, I spent an upaid eight hours designing the Vennebush Family Flag and playing Uno, Swish, and Qwirkle with the boys, while my gainfully employed wife dialed in to back-to-back-to-back conference calls. Moral: Check the forecast before quitting a job prematurely.
A Parting Gift
One of my colleagues at NCTM gave me a broken calculator. (And, no, this isn’t just a cheesy, elaborate set-up for a silly math problem.) The calculator used to be a normal, fully functioning, scientific calculator, but now it can’t add, subtract, multiply or divide without making an error. The good news is that the error is very predictable. The following video shows the results when using the calculator for four basic arithmetic problems.
The following (incorrect) results are shown in the video:
- 310 + 677 = 982
- 13 × 15 = 190
- 512 ÷ 64 = 3
- 75 – 10 = 60
And after the last problem, continual presses of the equal key should repeatedly subtract 10, but instead it shows consecutive results of 45, 30, 15, and 0.
Can you discern the pattern?
Math Jokes, Yo! Let It Snow…
If you live near northern Virginia, then you’re stuck inside on a snowy day. If you’re bored and need something to do, you could attempt to solve the snowplow problem from R. P. Agnew’s Differential Equations (McGraw-Hill, New York, 1942).
One day it started snowing at a heavy and steady rate. A snowplow started out at noon, going 2 miles the first hour and 1 mile the second hour. What time did it start snowing?
If you can’t find the solution easily (or if you think that the problem is unsolvable), don’t fret. This problem has befuddled students for 71 years.
If you’re not a masochist, though, then you may just like some math jokes for a snowy day.
Math Teacher: We’re going to have an exam tomorrow, rain or shine.
Student: Great! It’s snowing.What math do Snowy Owls study?
Owlgebra.
Or perhaps you enjoy jokes with more elaborate set-ups…
An elder in a Native American tribe is asked, “Will it be cold this winter?” Not wanting to appear ignorant, he tells them, “Yes, it will be cold this winter. I suggest you start collecting firewood to be prepared.” The tribe disperses immediately to start collecting wood. Meanwhile, the elder heads to a phone and calls the National Weather Service. He asks the person who answers, “Will it be cold this winter?”
The agent at NWS responds, “Yes, our early data indicates that it will be a cold winter.”
The elder returns to the tribe and tells them, “Keep collecting wood! A cold winter is on the way!” Just to be sure, the next day he calls NWS, and again he asks, “Will it be cold this winter?”
The agent responds, “Our data now suggests that the winter will be very cold.”
The elder informs the tribe, “It will be a very cold winter! More wood!”
Wanting to be certain that he is sharing correct information, he calls NWS again the following day. “Are you absolutely certain that it will be very cold this winter?”
“Yes!” says the NWS agent. “The Native Americans are collecting firewood at an unprecedented rate!”