Results of a Wonderlic-SAT Comparison

Eli Manning and Tom Brady are arguably the smartest pair of quarterbacks to face each other in a Super Bowl. That’s not just hyperbole; there’s data to support it. Manning scored a 39 on the Wonderlic test, and Brady scored a 33, giving them an average score of 36. That’s the highest average ever for the starting quarterbacks in a Super Bowl.

The two starting quarterbacks for Super Bowl XLVII, Colin Kaepernick and Joe Flacco, are no intellectual slouches, either. Flacco scored a respectable 27 on the Wonderlic, and Kaepernick rocked the test with a 37, placing him two standard deviations above the norm. That puts him in the 97th percentile. If he wins the Super Bowl this Sunday, he’ll be the second-smartest quarterback to do so.

Last week, I asked readers to supply me with data for a research project. The Wonderlic test is used by the National Football League to measure the problem-solving abilities of prospective players. The SAT (and the ACT) have long been used as college entrance exams, and both claim to predict college success. My hypothesis is that the Wonderlic — a 12-minute, 50-question test — would be equally good at predicting college success.

The following presents the (I) results, (II) limitations of the research, and (III) some notes about the methodology. (Sorry, I don’t mean to be pretentious or to imply false erudition by using Roman numerals. I just know that some folks are interested in (I) but could give a rat’s butt about (II) or (III), so I thought dividing this post into sections might be helpful. Hopefully by using the phrase “rat’s butt,” I’ve removed all sense of pretense.)

I. Results

Neither the SAT nor the Wonderlic are good at predicting college success, but to my surprise, the SAT is better than the Wonderlic.

The following correlation coefficients resulted when three pair-wise correlations were performed:

• Wonderlic and GPA: r = 0.0086
• SAT and GPA: r = 0.0506
• Wonderlic and SAT: r = 0.2897

When comparing the Wonderlic and college GPA (n = 46), the correlation coefficient was r = 0.0086, meaning that roughly 9% of the variance of college GPAs can be explained by Wonderlic scores.

When comparing the SAT and college GPA (n = 41), the correlation coefficient was r = 0.0506, meaning that roughly 22% of the variance of college GPAs can be explained by SAT scores.

When comparing the Wonderlic and SAT (n = 44), the correlation coefficient was r = 0.2897, meaning that roughly 54% of the variance of college GPAs can be explained by Wonderlic scores.

Though not quite as strongly, these results corroborate my previous findings that neither the SAT nor the Wonderlic is a very good predictor of college success, but both are pretty good predictors of scores on other standardized tests.

II. Limitations

A number of factors discredit the validity of this research, among them:

• Voluntary Response Bias. The majority of respondents were above average in all categories. Additional data is needed from individuals who scored poorly on the SAT/ACT or Wonderlic or who had below-average college GPAs.
• Sample Size. It is difficult to draw conclusions from a sample of just 54 individuals.
• Timing. Those who responded often took the Wonderlic many years after taking the SAT. This is an issue with data from NFL prospects, too; they take the SAT prior to entering college, but they take the Wonderlic at least three years later. Certainly, those years of experience would influence the results.
• Consistency. College GPA is not transferrable. Without a doubt, earning a 3.1 GPA at Harvard University is more impressive than holding a 3.9 at the Univerity of the District of Columbia. Even within the same university, there can be discrepancies; it’s likely more difficult to hold a high GPA if your major is electrical engineering than, say, parks and recreation. Unfortunately, it’s one of the only means of comparing two students from different schools, apart from reputation of the issuing institution.

Consequently, this research should be taken in the spirit it was intended. It it not academic research. It was merely a tongue-in-cheek attempt to show that neither the SAT/ACT nor the Wonderlic test are terribly good at predicting college success.

That said, this analysis could serve as the impetus for an academic research project. By gathering Wonderlic scores from high school students at the same time that they take the SAT, and then tracking them to determine their success in college, the viability of the Wonderlic test as a college entrance exam could be determined. (It should be noted that the Wonderlic Personality Test (WPT) is used by the NFL when evaluating prospective players, but scores on the Wonderlic Basic Skills Test (WBST) are already accepted by some colleges.)

III. Notes About the Method

For consistent comparison, all college exam scores were converted to a scale based on the old SAT (out of 1600). ACT scores were converted using results of a concordance study conducted by the ACT and the College Board. Converting scores from the new SAT to the old SAT used the method described below.

Because the maximum score on the new SAT is 2400 and the maximum score on the old SAT was 1600, the following conversion formula might seem reasonable:

2/3 × new SAT = old SAT

However, there are two reasons that won’t work. First, in addition to covering the same math topics as the old SAT, the new SAT also covers Algebra II. Second, the writing section has proven to be the hardest part of the new test; the average score on the writing section is 493, since its inception in 2005; by comparison, the average scores for math and reading are 516 and 501, respectively, during the same time period.

Using scores from 2000-11, it seems that approximately 67.3% of a student’s score on the new SAT comes from the math and reading sections; the writing section only accounts for about 32.7% of the student’s total score. Second, the average score on the old SAT from 2000-05 was 1024, whereas the average combined score for the math and reading sections on the new SAT from 2005-11 was 1017, which means that the average score on the old SAT was about 0.7% higher than the average combined score on the math and reading sections of the new SAT.

Consequently, for any respondent who listed a new SAT score, I multiplied their score by 0.673 to find their score on just the math and reading sections, and then I multiplied by 1.007 to account for the higher average score on the old SAT. This is obviously an imperfect system. That said, one of the respondents told me that his combined math/reading score on the new SAT was 1390, and this formula yielded an old SAT estimate of 1410. Since the old SAT score should be slightly higher, it seems that the formula is reasonable. I therefore used this formula for all respondents who listed a new SAT score, of which there were only two.

No changes were made to the college GPAs, despite the inherent flaws described above.

Once the data was in comporable form, my good friend Excel was used to perform a linear regression and determine the correlation coefficient.

Decimal Displacement

I used to dislike math, but then I realized that decimals have a point.

For instance, they separate dollars from cents in prices, as shown on the price tag of a Black Brown 1826 shirt that I received as a gift from my mother-in-law:

Like me, you may be wondering: Why would they include four zeroes instead of just two after the decimal point?

My first thought was that Black Brown 1826 was a London-based company. The tag shows the price in U.S. dollars, so it would make sense that a British company would display the price in U.S. dollars to four decimal places — currency pairs are often expressed to four decimal places.

But that’s not the case. Black Brown 1826 is a clothing line at Lord + Taylor, which is a North American company.

My second thought was that the designer of the line might be European. But nope. The line was designed by Joseph Abboud, an American designer.

My third thought was… well, actually, I didn’t have a third thought. And I still have no idea why the price is expressed to four decimal places.

Do you know why there would be four decimal places shown in the price? If you have a theory, leave a comment.

The location of the decimal point is often a mystery to kids, too, but not for this student…

A math teacher wrote 15.1 on the board. “This is what happens if we multiply by 10,” she said, and then erased the decimal point.

“Now where’s the decimal point?” she asked.

A student answered, “On the eraser!”

But decimal points can also pose problems for adults…

A colleague noticed a new spot on the carpet in the hallway. “Quick! Call the accounting department!” he yelled. “See if they misplaced a decimal point again!”

SAT, Wonderlic, and GPA

Yeah, that’s right. I’m as smart as Greg McElroy, and I’m smarter than Blaine Gabbert. Based on Wonderlic scores, anyway.

I scored a 43, so I guess that means I’m smarter than Phil Simms, too.

The Wonderlic test has been administered to NFL players since the 1970’s, and Phil Simms scored the lowest of all Super Bowl quarterbacks who have taken the test. He led the New York Giants to victory in Super Bowl XXI, but he only got a 10 (out of 50). A score of 10 indicates that a person is literate, but “that’s about all we can say,” according to Charles Wonderlic, Jr. And to think that Phil’s words will be heard by 100 million people when he announces Super Bowl XLVII on Feburary 3.

Ever wonder which NFL players are intellectually inferior to you? You can find out by taking the mini-Wonderlic test at www.nicholascreative.com/footballiq.

And I sure wish you would. Since conducting “research” for my Smart Quarterbacks post two years ago, I’ve been somewhat obsessed by the idea that the Wonderlic — a 12‑minute, 50‑question test — will someday unseat the SAT — an onerous, expensive, 5‑hour ordeal consisting of 10 sections — as the entrance exam for college.

In my wildest fantasies, I envision a world with no entrance exams. Not without reason, mind you. It’s just that the SAT is better at measuring natural intelligence than predicting college success. Then again, so is the Wonderlic. But the Wonderlic takes only 4% as long to complete, so high school students wouldn’t have to sacrifice an entire morning to complete it.

To prove my point, I attempted to gather SAT scores, Wonderlic scores, and college GPAs for a handful of NFL players, and this data has supported my hypothesis — that the Wonderlic test is just as accurate as the SAT at predicting college success (which is to say, it is equally abysmal). But the sample size is far too small to be reliable.

Data. I need more data. Data, data, data.

That’s where you come in.

If you’re willing, please enter your SAT (or ACT) score, your college GPA, and your Wonderlic score in the form below. (If you can’t see the form below, try this Google form.) All of this data will be held confidential. I will only use it to conduct an analysis.

You probably remember your SAT or ACT score and your college GPA. But you probably don’t know your Wonderlic score, because most people have never taken the Wonderlic test. you can take the mini-Wonderlic at www.nicholascreative.com/footballiq to get a fair approximation of your Wonderlic score.

Thanks in advance for your help. I’ll collect data through Wednesday, January 30, and I’ll post my analysis before kick-off on Super Bowl Sunday.

Once Removed, Twice Shy

Family relations are hard.

A man is holding a photograph of another man and says, “Brothers and sisters I  have none, but this man’s father is my father’s son.” Who is the man in the photo?

But you don’t need riddles to make confusing situations. Real life is difficult enough.

When Lynne Cheney was doing genealogy research for Blue Skies, No Fences, a memoir about growing up in Wyoming, she discovered an interesting tidbit: Barack Obama and Dick Cheney are cousins. In particular, both are descendants of Mareen Duvall, a Huguenot who immigrated from France and settled in Anne Arundel County, Maryland.

Based on her homework, Lynne Cheney claimed that they were eighth cousins. The Chicago Sun-Times, however, reported that they were ninth cousins once removed.

If either Cheney or the Sun-Times got it wrong, well, who could blame them? This whole business of nth cousins p times removed is a bit overwhelming.

The holiday season is a good time to review the rules for consanguinity. (Consanguinity, from the Latin consanguinitas, means “blood relation.” The first two syllables lead to the modern term cousin.) At holiday gatherings, it is not uncommon for discussions like the following to occur:

“Hey, who was that on the phone?”

“That was Johnny. You remember him, Uncle Lenny’s brother’s kid?”

“Oh, yeah! What is he, my third cousin?”

“No. He’s your second cousin.”

“Actually, he’s your first cousin once removed.”

“No, he’s not! He’s your great nephew!”

“????????”

It wasn’t until a recent family gathering that I realized (a) I ought to learn these rules about consanguinity so I could avoid these ridiculous conversations and (b) there’s got to be a simple mathematical formula to figure out the relationship between two people.

As it turns out, once I found the solution to (b), then (a) was pretty easy.

Figuring out the relationship between two people can be accomplished with the following algorithm.

1. Make an ascent list for each person. An ascent list is a list of ancestors proceeding from each person to their parents, to their grandparents, to their great-grandparents, and so on.
2. Determine the first ancestor common to both ascent lists.
3. Express the common ancestor in the form G^xP and G^yP for each person. Then, the two people are nth cousins p times removed, based on the following:
   

Some notes about this algorithm:

• The values of x and y depend on how many G’s appear in the relationship. For instance, a grandparent would be G¹P, but a great-great-great-grandparent would be G⁴P.
• The algorithm works for x = 0 or y = 0, either of which would indicate a parent.
• If n = 0, the relationship between the two people is sibling (p = 0), niece/nephew (p = 1), great niece/nephew (p = 2), and so on.

As an example, let’s say that you and Johnny are trying to figure out how you’re related. Your great-great-grandmother (G³P) is Johnny’s grandmother (G¹P), so x = 3 and y = 1. Then

and

which means that Johnny is your first cousin twice removed.

According to geni.com, Barack Obama is the 9th great grandson of Mareen Duvall and Dick Cheney is the 8th great grandson of Mareen Duvall. If that’s correct, then x = 9, y = 8, and Obama and Cheney are eighth cousins once removed.

And if that’s the case, then neither the Chicago Sun-Times nor Lynne Cheney got it correct. (See, I told you this sh*t was hard.)

If you really want to geek out on the mathematics of consanguinity, check out http://www.knotsystem.dk/TheKnotSystem.pdf.

MJ4MF Featured in MTaP 58

Let’s Play Math is hosting Math Teachers at Play 58, a blog carnival for math teaching and learning. This month’s issue includes two puzzles, links to at least 50 math blogs, and nine jokes that Denise borrowed from the MJ4MF blog.

What’s special about 58? Well, not much, except that it’s the minimum wind speed (in miles per hour) needed to issue a severe thunderstorm warning, it’s “the luckiest number ever” according to Patrick from SpongeBob SquarePants, and it’s an 11‑gonal number:

I highly encourage you to check out Math Teachers at Play 58, even if you’re not a teacher. But don’t go for the jokes; if you read this blog, you’ll have seen them all before. As it says at the carnival, “If you like to learn new things and play around with ideas, you are sure to find something of interest.” Sounds good to me. Enjoy!

A New Tattoo

I was both nervous and excited when I walked into the tattoo shop. I had been working extra hours in the tutoring center to save for this, and the moment had finally arrived. Sure, I could have played it safe and asked for a tribal pattern on my upper arm. But I’ve always lived by the mantra, “Go big, or go home.”

“What are we doing today?” the tattooist asked.

“How about x + 6 across my left cheek?” A blank stare. “You know, like from algebra,” I explained.

I got the sense he wanted to ask some follow-up questions… but then decided against it. Instead, he started inking. Twenty minutes later, he held up a mirror so I could see his handiwork.

“You don’t like it, do you?” he asked.

“No, no, I love it!” I said. “What makes you think I don’t like it?”

“I can tell by the expression on your face.”

Serious Math, Seriously…

“Patrick, I have to ask you a question,” said Martha. “You have written a book of math jokes… so, how are you so very serious?”

In my 41.82 years, this is the first time that anyone had ever used the word serious to describe anything about me.

Clearly, Martha doesn’t know me.

Then again, perhaps Martha’s perception is based on me doing things like stating my age as a decimal to the nearest hundredths.

Martha and I had only been introduced two days earlier. We were both asked to participate in a quality review session for the Math Snacks project at the Learning Games Lab at NMSU — which, by the way, is a great project; I particularly like the Bad Date video and the Gate video game — so she hadn’t really had much time to get to know me.

But it made me wonder… do other people think I’m too serious, too?

To correct this false perception, here are some non-serious things I’ve done:

• I regularly pretend that one button is broken on my calculator, and then have to figure out alternate methods to calculate the value of long expressions. (On one particularly zany day, I pretended that two buttons were broken. Boy, did that ever lead to some crazy misadventures!)
• One afternoon — when the curtains were not drawn — I danced if no one were watching. The tune that put my backfield in motion? New Math by Tom Lehrer.
• I once used the phrase “backfield in motion” in a math blog post.
• In an academic paper submitted to a prestigious journal, I once reported a result to three significant figures, even though I was well aware that only two significant figures were justified.
• At a bookstore, I paid for a copy of Innumeracy entirely with pennies.
• On my way to a lecture, I asked a passer-by for directions to the lecture hall. She pointed straight ahead… and I turned around and walked the other way.
• I regularly wear a hat that reads, “Shut your πhole.”
• When someone enters the elevator and says, “Seven, please,” I push the 2 and 5 buttons and say, “There ya go. That makes 7.”
• When a telemarketer asks, “How are you doing?” I usually say, “I’m great, thanks. And I’m glad you called, because — boy! — do I have an exciting offer for you! Do you like to laugh? Do you like math? For $12 — or the cost of just two venti, non-fat, no foam, no water, six pump extra, hot chai tea lattes at Starbucks — you can have a personally signed copy of Math Jokes 4 Mathy Folks delivered right to your door! That’s right, just $12! How many copies can I put you down for?”

Gee, I sure hope Martha reads this…

Math of iPhone 5

Math teachers across the country are cringing. Everyone knows that you shouldn’t write it as iPhone 5. The correct format is 5i · Phone.

I overhead a teenager tell his friend that the iPhone 5 is “unreal.” Not exactly, punk. The proper term is imaginary.

Math Dreams

“I can’t get the numbers to stop.”

That’s what Eli told my wife tonight when he woke from a bad dream.

I once had a dream where I was afraid of numbers, too. During the week leading up to my midterm in Linear Algebra, I was reviewing problems from old exams. Though I thoroughly understood all that had been covered in class, and though I was able to complete all the exercises from the textbook with aplomb, I was only getting about 25% of the questions on the old exams correct.

It was freaking me out, and the night before the exam, I went to sleep very nervous.

My sleep was broken by a nightmare in which numbers were flying past my head like cannonballs from a numerical howitzer. They were coming from every direction. To make matters worse, my head was being squeezed by the brackets of a matrix as if it were in a vice.

I woke in a cold sweat. It was 5 a.m. Too anxious to sleep any more, I went to a study carrel in the library where I read and re-read the textbook and continually tried the problems from the old exams. I skipped my morning classes and studied for five straight hours. Yet I was still only able to get a quarter of the problems correct.

The midterm was at 12:30 p.m. At 11:55 a.m., I saw a woman from my class. Though I had never spoken to her before, I approached her and said, “Excuse me, aren’t you in Dr. Sibley’s linear algebra course?”

“Yes,” she replied skeptically.

“Would you mind helping me?” I asked, embarassed by the question.

“Uh… sure,” she said.

I asked her a few questions about the topics we had covered. She confirmed that I understood the material correctly. “So why am I missing so many of the questions from the old exams?” I asked rhetorically.

She took a look at my work and confirmed that it, too, was correct. Then she revealed the punch line: The professor had given us a packet of six exams, and the answer keys for all six exams were copied onto a seventh sheet. But the answer keys and the exams were not in the same order — each answer key had to be matched to an exam by noting the semester and date on each.

Arrgh.

I was relieved. Yet frustrated. I managed an 85 on the midterm… yet I’m certain I would have aced it had I gotten a good night’s sleep.

Mark Jason Dominus has much better math dreams than I. He posted the following problem to the mattababy listserv. He claimed that it came to him in a dream; when he woke, he thought it was still a good problem, so he decided to share it.

The volume of a 3 × 3 × 3 cube is 27 cubic units, and the volume of a 2 × 2 × 1 prism is 4 cubic units. Theoretically, six prisms should be able to fit inside the cube, with three cubic units empty. But can you arrange six 2 × 2 × 1 prisms so they fit inside a 3 × 3 × 3 cube?

Friends of mine who taught at the Center for Talented Youth claim that M. J. Dominus would often arrive late to the evening study sessions. As the story goes, he would take naps after dinner… if his alarm sounded while he was in the middle of a math dream, he would shut off the alarm and return to sleep so he could finish whatever mathematical proof his subconscience had been working on.

Wow.

What’s the scariest or coolest math dream you’ve ever had?

Swish, Swash, I Was Doin’ Some Math

I’m not sure what I want to be when I grow up, but I know who I want to be. That would be Bill Ritchie, owner and founder of Thinkfun^®, a company that makes and markets games and puzzles, including the wildly popular Rush Hour^® game.

Our house has recently become addicted to Swish^TM, one of Thinkfun’s newest games. Swish is a spatial card game played with transparent cards that can be rotated and flipped to make swishes. Swishes — named after the sound made by a perfect basketball shot going through the net — are made by layering as few as two or as many as 12 cards so that every ball swishes into a hoop of the same color.

For instance, the two cards below can be combined to make a swish. The orange dot on the left card aligns with the orange hoop on the right, and the blue hoop on the left aligns with the blue dot on the right, which forms a double swish when the cards are placed one on top of the other.

Here’s a more advanced example. These four cards can be layered to make a quadruple swish:

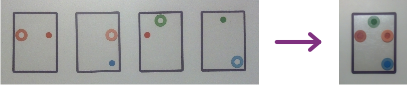
The examples above show the cards in perfect alignment. They just have to be placed one on top of another for the dots and hoops to align. What makes the game fun and challenging is that cards typically aren’t in perfect alignment like this. One or more of the cards will have to be flipped or rotated to make a swish. In addition, the set-up arranges 16 cards in a 4 × 4 grid, so the two complementary cards are rarely next to one another. Consequently, the game uses all three geometric transformations — reflections, rotations, and translations.

Each card contains one hoop and one dot. These two objects are placed in one of 12 regions — each card is divided into an imaginary 4 × 3 grid. Theoretically, it’s possible to make a 12-tuple swish… though I’ve yet to pull off such a feat during a game.

There are a number of interesting math questions that can be asked about the game:

• Will there always be a swish in any 4 × 4 array of cards?
• The deck contains 60 cards. Does that account for every possible combination of hoops and dots? [The answer is obviously no, but that leads to some interesting follow-up questions.] How many different cards are possible? Finding the total isn’t as trivial as it sounds, since cards can be rotated or flipped; duplicates need to be removed. Which cards were included in the deck, which ones were excluded, and why?
• How many different double swishes can be formed by the cards in the deck? How many triple swishes? … How many 12-tuple swishes?

I don’t have answers to all of those questions yet. But I look forward to discussing them (and others) when I introduce Swish to some colleagues at an upcoming math conference!