Multiplicative Dates

If you read the previous post containing Math Problems for 2024, then you already know what a multiplicative date is. But in case you missed it, here’s the definition again:

A multiplicative date is one in which the product of the month and date is equal to the (two-digit) year. For instance, today — January 24, 2024 — is a multiplicative date, because 1 × 24 = 24.

The question I asked in that previous post was, how many multiplicative dates will there be in 2024?

But I’m revisiting this topic again today, because today is the first multiplicative date of a year that has more multiplicative dates than any other year this century. That’s right, no year 20XX has more multiplicative dates than 2024.

Of course, there’s no reason to stop there. There are quite a few interesting questions related to multiplicative dates:

1. How many years this century have no multiplicative dates?
2. Which two consecutive years have the most multiplicative dates combined?

Math Problems for 2024

The calendar is about to change again, and another year of possibilities lies before us. While there are many things that you might do this year, I beg you, please, do not find the sum of all odd positive divisors of 2024. It’s two gross!

There are many interesting problems that involve the number 2024. Enjoy!

• A “multiplicative date” is one in which the product of the month and date is equal to the (two-digit) year. For instance, August 3 is a multiplicative date in 2024, because 8 × 3 = 24. How many multiplicative dates will there be in 2024?
• Create a polygon whose perimeter is 2024 units and whose area is 2024 square units.
• The sum of the digits of 2024 is 2 + 0 + 2 + 4 = 8, and 8 is a factor of 2024. For how many numbers in the 2020s is the sum of the digits a factor of the number?
• The number 2024 is an iban number, because the English name for the number “two-thousand twenty-four” never contains the letter i. (It has no relationship to the banking term IBAN, which stands for “International Bank Account Number.” It also only applies to the standard English names for numbers, not special names like googol or Kaprekar’s constant.) What is the largest iban number?
• What is the sum of 1 + 2 + 3 + 4 + ··· + 2024?
• What is the sum of 2 + 4 + 6 + 8 + ··· + 2024?
• What is the sum of 13 + 26 + 39 + ··· + 2024?
• How long would it take you to count to 2024?
• Using only common mathematical symbols and operations and the digits 2, 0, 2, and 4, make an expression that is exactly equal to 100. (Bonus: make an expression using the four digits in order.)
• All possible four-digit numbers that can be made with the digits 2, 0, 2, and 4 are formed and arranged in ascending order. What is the median of those numbers?
• What fraction is equivalent to 0.2024?
• How many positive integer factors does 2024 have?
• Create a 4 × 4 magic square in which the sum of each row, column, and diagonal is 2024.
• What is the units digit of 2024²⁰²⁴?
• Each dimension of a rectangular box is an integer number of inches. The volume of the box is 2024 in³. What is the minimum possible surface area of the box?
• What is the maximum possible product for a set of positive integers that have a sum of 2024?
• A polynomial p has non-negative integer coefficients and satisfies p(1) = 8, p(-1) = 0, and p(3/2) = 13.75. What is p(10)?
• Let S(n) denote the sum of the digits of integer n. For example, S(123) = 6. Find a number n such that n + S(n) + S(S(n)) + S(S(S(n))) = 2024.

Special thanks to Professor Harold Reiter for supplying the last two problems in the list.

[Update 12/31/23] Too beautiful not to share, this truth about the year was posted in the Wolfram Community by Ed Pegg of Wolfram Research:

2³ + 3³ + 4³ + 5³ + 6³ + 7³ + 8³ + 9³ = 2024

And this representation appeared in a post about math beauties of the new year at Math 1089:

2024 = 1 − 2 + 3 × (4 + 5) × (6 + 78 − 9)

Awesome.

A Tent for n Persons

Over 58 million households went camping in 2022, and almost half of them camped 3 or more times during the year. With the number of campers and camping nights increasing as a result of the pandemic, it’s no surprise that campgrounds are full in 2023. The good news is, it’s relatively easy to determine the capacity of a campground.

How many tents can fit in a campground?
Ten. Because ten tents make one whole!

To make that joke work, you have to mispronounce “tenths” as “tents,” so it’s helpful if you speak like My Cousin Vinny (“the two yutes”).

What’s more difficult, though, is determining the capacity of a tent.

Sometimes, the listed area is very generous. For instance, the Pacific Pass Two‑Person Family Dome Tent offers a spacious 24 square feet to each inhabitant. By comparison, campers in the North Face Wawona 6 Tent are bound to feel a little cramped with just 14 square feet per person.

Then there’s the ambiguous Moon Lence 4-5 Person Family Camping Tent that gives a range of 4‑5 people in the name, lists an occupant capacity of five people in the specifications, and says it’s a “roomy four-person tent” in the description. WTF? Moreover, the floor has an area of just 58 square feet, so each person would get less than 15 square feet if there were four people and less than 12 square feet if inhabited by five people; and, with its cool but impractical pentagonal shape, two of them would need to sleep in the fetal position.

So, what is the right amount of space per person? It’s hard to say. According to manufacturers, though, it seems to be about 15 square feet. That estimate is based on data from 26 tents that yield the following line of best fit:

With a coefficient of 15 associated with the independent variable, the regression equation implies that each camper needs about 15 square feet of sleeping area.

I’m not buying it, though. Tents never seem to have enough area for the number of people they claim to fit. Theoretically, our family tent will comfortably sleep three people, but in practice it’s plenty crowded with just two, and sometimes there shouldn’t be more than one — especially if that one suffers from sleep apnea or had burritos for dinner.

Should you need a tent, I recommend you wait till after camping season. You’re more likely to find a good deal when there’s snow on the ground, during the winter of discount tents. If the camp store offers you insurance, however, you should decline it. Were someone to steal your tent while camping, you wouldn’t be covered. And sometimes, the camp store will put tent pegs on the highest shelf; sometimes, the stakes are just too high. Should a bunch of crows accompany you on a camping trip, that would be murder within tent.

Finally, I have to ask:

Is a tent two-and-a-half-times as large as a fort?

I’d Like a Wordle with You

Okay, fine, if no one else will say it, then I’ll say it: Wordle is a pain-in-the-ass.

I know, I know. It’s probably political suicide to denigrate the most popular word game on the planet, but if speaking truth to power means I’ll never be the Archbishop of Canterbury or a member of the Delaware Chancery Court, well, so be it.

There are two aspects of Wordle that are a tempest in a teacup:

• First, solving the puzzle in just one or two guesses is largely a matter of luck. In and of itself, this is not a problem. Rather, it’s the braggarts on social media who ascribe their success to intelligence rather than serendipity that really grinds my gears.
• Second, the Wordle app contains a fundamental flaw. If life intervenes and causes you to miss a day — perhaps because you’re on a canoe trip with no internet service; or, you’re visiting Green Bank, West Virginia, where cell phones and wi-fi are illegal; or, you’re perilously close to proving the Riemann hypothesis and are afraid to pause and lose focus — then your Wordle streak is reset and you’re required to begin anew. Personally, I think the streak should only reset if (a) you fail to find the word in six guesses or (b) you fail to find the word using one or more guesses before the next puzzle appears on the following day.

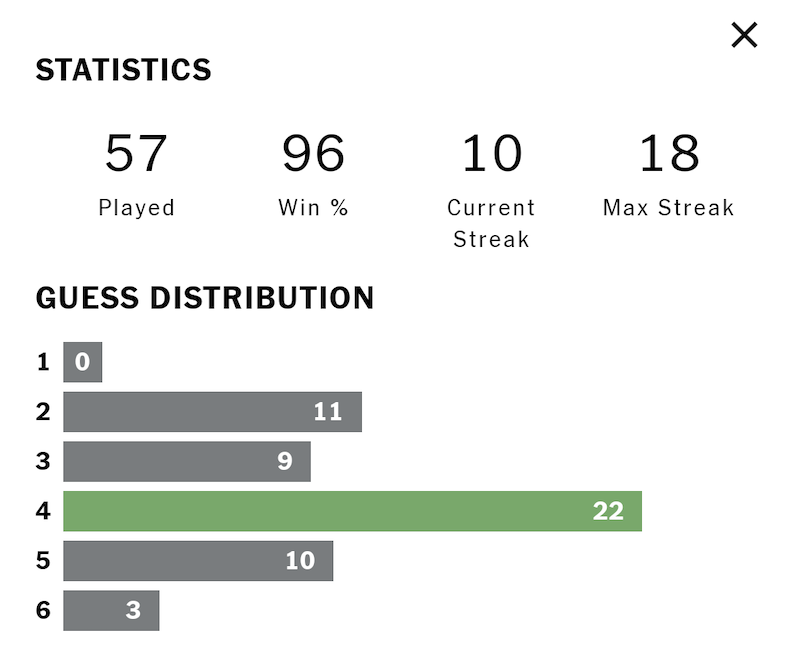
For me, there is no joy in finding the word in just two guesses; but, there is utter devastation if the correct answer isn’t found in six guesses. Sadly, I’ve twice failed to find the word:

This, of course, leads to a math problem:

As shown above, I’ve played 313 games, and I’ve solved 5 + 59 + 158 + 72 + 17 = 311 of them. Consequently, the Wordle app displays my Win % as 99. Assuming typical rules of rounding, how many puzzles will I need to solve (without a miss) so that it displays my Win % as 100?

My wife takes great joy in finding the word in just two guesses, so for her, occasionally failing to solve the puzzle in six tries is a fair tradeoff. But her risky strategy means that her Win % suffers a bit:

Though I’ve played six times as many games, she’s solved the puzzle in two guesses more than twice as many times as I have.

But despite its imperfections, I’m still addicted to Wordle.

One of the reasons is that the statistics surrounding Wordle permit interesting birdwalks for math geeks. To wit, the Wordle database allegedly contains 12,545 allowable words but only 2,309 possible answers. If you randomly guess one of the allowable words, you have a 0.008% chance of finding the word on your first guess; instead, if you randomly guess one of the possible answers, you have a 0.04% change of finding the word on your first guess. So, how have Wordle players been able to guess the answer on their first try more than 0.02% of the time?

Another reason for my addiction is my love of anagrams.

For your puzzling pleasure, here are some anagram puzzles for you. The first is about my favorite four-letter anagrams.

The letters S, T, O, and P can be combined to form 24 different arrangements. Amazingly, six of them are actual English words! Can you find them all?

The next four puzzles all have to deal with anagrams of names.

The name CAMERON has only one anagram, but oh, what a beautiful word! Can you find it?

The letters of the name ANDREW can be rearranged to create three other words. Can you find all three?

When I meet someone new, I take it as a personal challenge to find an anagram of their name. Sometimes, though, an anagram just doesn’t exist. Which of the following names cannot have its letters rearranged to form a common English word?

• ANNIE
• ARTIE
• BRIAN
• CARSON
• DEEPAK
• DANIEL
• ELISA
• LISA
• MATTHEW
• NEVAEH
• TIARET

(This is a true story.) A mother named ANIDA wrote to babynames.com and said she planned to give a name to each of her children that was an anagram of her own name. How many can you come up with? Admittedly, some of her suggestions aren’t terribly common. But what’s in a name, anyway? (Head to babynames.com to see her letter and her list of names.)

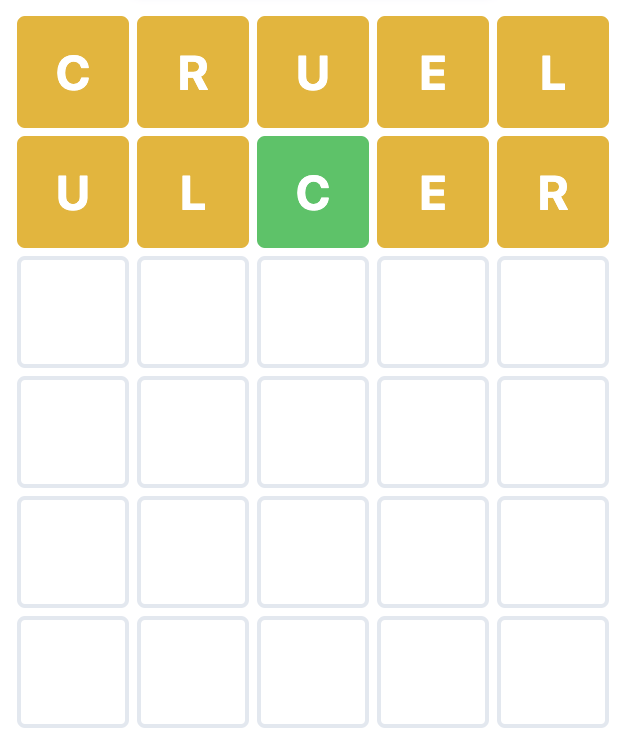
Finally — but not least importantly — allow me to introduce you to the Make Your Own Wordle generator at Strive Math. Using that site, some five‑letter anagrams were used to show a few Wordle games already in progress. For each of the puzzles below, you should be able to get the word on the next guess. (Amazingly, there are six possible anagrams of the letters A, E, L, S, and T for Puzzle 3, but the answer is uniquely determined after just these two guesses.)

Puzzle 1. Three guesses, three correct letters. What’s the word?

Puzzle 2. Two guesses, one correct letter. What’s the word?

Puzzle 3. Two guesses, zero correct letters. What’s the word?

The six anagrams of S, T, O, and P are OPTS, POST, POTS, SPOT, STOP (duh!), and TOPS.

ROMANCE is the only anagram of CAMERON.

The letters of ANDREW can be rearranged to form WANDER, WARDEN, and WARNED.

Only MATTHEW can’t be rearranged to form a common English word. (If you can’t find anagrams of the others, use the oldest and, in my opinion, the best anagram generator on the web.)

The letters of ANIDA can be arranged to make quite a few names: AIDAN, DIANA, DAIAN, NADIA, DANIA, DAINA, ADINA, NAIAD, and probably many others.

And the three Wordles are solved with NOTES, LUCRE, and STEAL.

See you in three months, when I’ll hopefully be able to display a Win % of 100.

Guess the Graph on Derangement Day

Today is 4.1.23, a date in which the digit 4 occupies the first position, the digit 1 occupies the second position, the digit 2 is in the third position, and the digit 3 is in the fourth position. That is, no digit n is in the nth position. In mathematics, we call this a derangement, a permutation of the elements of a set such that no element appears in its original position. Using the same format, when will the next “derangement day” occur?

Today also happens to be April Fools Day. If pranks are your thing, then here’s a math prank for you:

What is the product of all single-digit prime factors of 143?

Why is it a prank? Because the prime factors of 143 are 11 and 13, neither of which is single‑digit. So, the set of all single‑digit prime factors of 143 is the empty set { }, which means it contains no elements. Since there are no elements in the empty set, the product of the elements should be 0, right? Well, not exactly. By convention, the product of the elements of the empty set is 1, though it might be more precise to say that the empty product is the multiplicative identity.

But my apologies for that discursion. Let’s return to the reason for today’s post.

Today is also the day when the two semifinal games of the NCAA Men’s Basketball Tournament will be played. Three teams that have never made it this far before — Florida Atlantic, San Diego State, and Miami (FL) — join UConn in the Final Four. And that leads to the math question of the day: identifying the data set that was used to construct the bar graph below.

click to enlarge the image for a better view of the axis values

The omission of axis labels and chart title was deliberate. What should they be?

That’s a big question. Maybe too big. Let’s start with two smaller questions.

What do you notice?

• Did you notice that the bars are clustered together?
• Did you notice that there are gaps?
• Did you notice that 0 occurred most frequently, and that the bars generally decrease in size from left to right?
• What else did you notice?

What do you wonder?

• Do you wonder if the graph was horizontally truncated, and maybe there are some bars with category values greater than x = 60? (Ooh, good question! There aren’t; none of the data had a value greater than 55.)
• Do you wonder why the bars only occur when the units digit is 0‑5? Or why no bars occur when the units digit is 6‑9?
• Do you wonder why I spend so much time asking annoying, rhetorical questions? (Yeah, me, too.)
• What else do you wonder?

Take a minute to analyze the graph and think about those questions. What are your initial thoughts for the data set that was used to create it? Make a first guess at what the axis labels and chart title might be.

Okay, now some hints. I mentioned above that today is the Saturday of the Final Four, so perhaps you already thought that the graph might have something to do with college basketball. If so, you’d be right.

Not enough? Then let me divulge that the data set used to create this graph contains 320 elements.

Still not enough? Don’t sweat it. This is a tough one. Your final hint is that 320 = 64 × 5.

Okay, time to let the cat out of the bag. March Madness includes 64 teams (if you don’t count the play‑in games, and — because I’m a purist, or because I’m old — I don’t). Further, every coach identifies 5 starters for each game. The 320 elements in the data set are the uniform numbers for the 5 opening-round starters from each of the 64 teams. In college, basketball uniform numbers are not allowed to include the digits 6, 7, 8, or 9. Specifically, under Rule 1, Section 22, Article 7, Clause b.2 of the NCAA Men’s Basketball Rules Book, “The following numbers are legal: 0, 1, 2, 3, 4, 5, 00, 10, 11, 12, 13, 14, 15, 20, 21, 22, 23, 24, 25, 30, 31, 32, 33, 34, 35, 40, 41, 42, 43, 44, 45, 50, 51, 52, 53, 54, and 55. Team rosters can include 0 or 00, but not both.” Why does this rule exist? To help the person keeping score. No, seriously. When a player commits a foul, the referees signal the player’s uniform number to the scorer’s table using their fingers. If a player wearing 51 committed a foul, the ref might display this:

So, you think you’re the perfect college basketball player? Sorry, you can’t wear 6 or 28. You think you’re a prime-time player? Too bad, you can’t wear 7, 17, 19, 29, 37, 47, 59, 67, 79, 89, or 97. Is your last name Kaprekar? You’re outta luck, you can’t wear 9 or 99. (I know, that’s a deep cut. Look it up.)

[Update, 4/5/23] On 4/1/23, when I asked when the next derangement day would occur, it was nothing more than an innocent question. Honestly, I hadn’t even considered what the answer might be, and I thought maybe one of the readers would posit a suggestion. But as I lay in bed this morning — thinking about the math of the date, as I’m wont to do — it occurred to me that today could be considered a derangement day.

Today’s date is 4/5/23, and the digits form the set {2, 3, 4, 5}. None of the digits in the date occupy the same location in the set. For instance, the digit 4 is the first digit in the date, but it’s the third element in the set. Consequently, this might be considered a derangement day. By that logic, tomorrow, Friday, Saturday, and Sunday this week would also be derangement days.

But I don’t love that. I feel like a derangement day should contain the digits 1‑n. But I never stated that. Perhaps all we really need is a better definition of derangement day, so here it is:

A derangement day is a calendar date that contains distinct digits 1‑n such that the digit k never occurs in position k of the date.

But even in that case, the next derangement day isn’t so far away. It occurs in just 10 days: 4/15/23. In that date, the digit n never occurs in the nth position.

The Triple Crown

I once heard the hosts on a sports talk radio show ask rapper and music exec Rick Ross to confirm the rumor that he mows his own lawn, because he gets his best ideas while cutting the grass. Ross replied, “Fact! Shout out to John Deere!”

More recently, I learned that John Deere and Co. posted worldwide revenue of $52B in FY22, a record for the farm equipment company.

Well, as the Romans said with just three little words, omne trium perfectum, so here goes…

If you don’t like geometry, then you don’t want to talk to that guy in the John Deere hat. He’s nice enough, but he’s pro-tractor.

The manure spreader is the only piece of equipment that John Deere won’t stand behind.

Did you hear about the woman who left her husband for a tractor salesman?
She wrote him a John Deere letter.

And here are my three favorite math signs:

And, finally, some random math jokes that involve the number three:

There are three kinds of people: those who are good at math, and those who aren’t.

Why do teenagers travel in groups of three?
Because they can’t even.

What’s a mathematician’s favorite candy bar?
n Musketeers, where n = 3!

How many ears did Alexandre Dumas have?
Five. A left ear, a right ear, and three musketeers.

If you like things that come in threes, you may appreciate Rob Eastaway and Jeremy Wyndham’s book, Why Do Buses Come in Threes? (This is not an affiliate link, just an unsolicited suggestion. Enjoy if you so choose.)

Sidhu Moose Wala Would Love This Post

[Sidhu Moose Wala – 47]

The following is a modified version of a problem that appeared in Concept Quests, a collection of problems originally written by Kim Markworth and soon to be offered by The Math Learning Center as a supplement to Bridges in Mathematic Second Edition.

I was today years old when I realized that I’ve been alive for 47 years, 47 months, 47 weeks, and 47 days. How old will I be on my next birthday?

Incidentally, the number 47 was also featured in this week’s challenge on the NPR Sunday Puzzle:

Take this equation: 14 + 116 + 68 = 47. Clearly this doesn‘t work mathematically. But it does work in a nonmathematical way. Please explain.

The number 47 is very interesting, especially if you’re a member of The 47 Society. But even if you aren’t, the number 47 has some noteworthy credentials:

• The number 47 is a safe prime, meaning it has the form 2q + 1, where q is also prime.
• The greatest number of cubes (not necessarily the same size) that cannot be rearranged to form a larger cube is 47. That is, it’s not possible to make a cube from 47 smaller, not-necessarily-the-same-size cubes, but it is possible to make a cube from 48, 49, 50, 51, or any greater number of cubes.
• 47 = 2⁵ + 5² – 2 × 5
• Lord Asano Takumi’s followers swore to avenge his death — a suicide he was obliged to commit for drawing his sword in the palace — and survives in a story known as the Legend of the 47 Ronin.
• Mexican revolutionary Pancho Villa was killed by 47 bullets.
• It takes 47 divisions of one cell to produce the number of cells in the human body; that is, there are approximately 2⁴⁷ cells in a human.
• Proposition 47 of Euclid’s Elements is the Pythagorean theorem.
• The Bible credits Jesus with 47 miracles.
• The Declaration of Independence has 47 sentences.
• There are 47 strings on a concert harp.
• The tropics of Cancer and Capricorn are located 47 degrees apart.

This fascination with the number 47 seems to have started a long time ago.

In the summer of 1964, two students at Pomona College — Laurens “Laurie” Mets and Bruce Elgin — began an extracurricular experiment to determine how often the number 47 occurred in nature. While this may seem like an odd thing to do, they weren’t the only ones; a number of Pomona students were involved in a summer program sponsored by the NIH, and many of them conducted similar experiments about the occurrence of random numbers, questioning the existence of patterns in nature. However, it was Mets’s and Elgin’s search for 47 that took on a life of its own and developed a cult following.

The experiment was to determine if 47 showed up in nature more often than other numbers. As a first step, they hypothesized that 47 would appear in two percent of all California license plates, which would be higher than would occur by random chance. According to Mets, a funny thing happened: when they looked at a bunch of license plates and counted the occurrence of 47, they found their hypothesis to be true. According to Elgin, however, the license plate experiment was a failure; but, within the next week, he saw a Rolaids commercial claiming that Rolaids absorbs up to 47% of its weight in excess acid. That sparked a desire to see where else 47 might occur… and before long, people all over campus were counting everything to look for 47s.

As part of that same summer program, statistician Donald Bentley gave a talk in which he stated that any number could be shown to be equal to any other number. In his (invalid) proof, he chose to show that every number was equal to — you guessed it — 47. How did he prove it?

Consider an isosceles right triangle for which the base is 47 units, and the congruent legs are each 37 units. Now, connect the midpoints of the congruent sides to the midpoint of the base, as shown in Figure 1. The combined lengths of the red segments in Figure 1 is the same as the sum of the lengths of the congruent sides, 74 units. Then repeat, connecting the midpoints of these smaller triangles, as shown in Figure 2. Again, the combined lengths of the red segments is 74 units. Then do this again and again and again — all the way to infinity — and eventually the triangles will get so small that the red segments will appear to be a straight-line segment that overlaps the base of the triangle, as shown in Figure 3. The length of the red segment is 74 units, and length of the base is 47 units, so 74 = 47. By similar (incorrect) reasoning, it would be possible to show that any number is equal to 47.

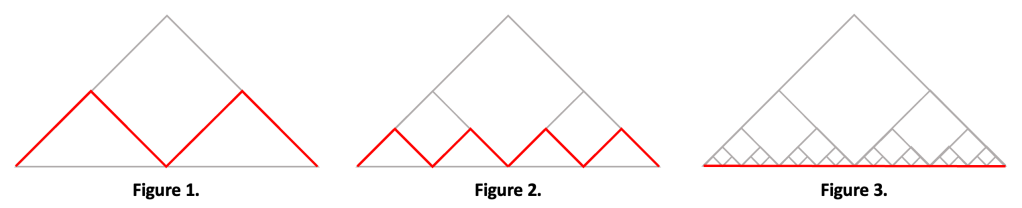
Although Dr. Bentley’s proof was meant as a classroom lesson on statistical computing, leave it to the 47-hunters to accept the proof and believe that all numbers equal 47.

(If you’d like to know more about this sordid history of 47, you can read The Mystery of 47 at the Pomona College website.)

Anyway, where was I? Oh, yes… I’ve been alive for 47 years, 47 months, 47 weeks, and 47 days.

Mathematically, what I find most interesting is the general case. That is, if I’ve been alive for n years, n months, n weeks, and n days, how old will I be on my next birthday?

For the problem I presented at the top of this post, n = 47, and the answer is 52 years; that is, I’ll turn 52 on my next birthday. But if n = 48, I won’t turn 53 on my next birthday; I’ll turn 54. That’s right, it skips a year. This happens periodically, and with a little help from the Date Calculator at www.timeanddate.com, I was able to generate this beautiful — albeit incomplete — graph:

 If you’re interested in seeing the data, check it out at https://www.desmos.com/calculator/u43gz6ahyi.

Something really wacky happens when n = 38. I was born on March 17, 1971, and the date 38 years, 38 months, 38 weeks, and 38 days from my date of birth was exactly 42 years later: March 17, 2013. Whoa.

Who knows what any of this means? Perhaps this implies that 38, not 47, is a magical number. In any case, I hope you have fun playing with this scenario and seeing what you can discover.

If that’s not your thing, though, here are some time-and-date jokes for you:

How many seconds are in a year?
Twelve. January 2nd, February 2nd, March 2nd, …

Did you hear about the hungry clock?
It went back four seconds.

Traditional calendars are for people who are week-minded.

I was fired from my job at the calendar factory. My boss was mad that I took a few days off.

Math Problems for 2023

Happy New Year!

I’m feeling lucky about 2023… but perhaps that’s because 7⁷ mod 7! = 2023.

But I’m also feeling lucky because there are many interesting problems that involve the number 2023. I’m a little late in getting this post out, but all of the following problems attempt to use the number 2023 in some interesting way. Thanks to Professor Harold Reiter from UNC‑Charlotte, who supplied the ideas for the first two problems; the rest are MJ4MF originals. Enjoy!

• For 2023, the sum of the digits of the year, times the square of the sum of the squares of the digits, is equal to the year itself. Yeah, that’s a mouthful; more concisely, (2 + 0 + 2 + 3) × (2² + 0² + 2² + 3²)² = 2023. Can you find the only other four-digit number abcd with the property that (a + b + c + d) × (a² + b² + c² + d²)² = abcd?
• If you place one dot inside an equilateral triangle and connect it to each vertex, you get three non-overlapping triangles. Similarly, if you place two dots in an equilateral triangle — and no subset contains three collinear dots — you can connect the dots to form five non-overlapping triangles. How many non-collinear dots must you place inside the triangle to get 2023 non-overlapping triangles?
• The sum of the digits of 2023 is 2 + 0 + 2 + 3 = 7, and 7 is a factor of 2023. For how many numbers in the 2020s is the sum of the digits a factor of the number?
• In how many ways can a 4 x 4 grid be covered with monominos and L-shaped triominos? One such covering is shown below.

• What is the sum of 1 + 3 + 5 + 7 + ··· + 2023?
• How long would it take you to count to 2023?
• Using only common mathematical symbols and operations and the digits 2, 0, 2, and 3, make an expression that is exactly equal to 100. (Bonus: make an expression using the four digits in order.)
• All possible four-digit numbers that can be made with the digits 2, 0, 2, and 3 are formed and arranged in ascending order. What is the first number in the list?
• Place addition or subtraction symbols between the cubes below to create a true equation:

9³     8³     7³     6³     5³     4³     3³     2³     1³ = 2023

• Find a fraction with the following decimal equivalent.

• How many positive integer factors does 2023 have?
• Create a 4 × 4 magic square in which the sum of each row, column, and diagonal is 2023.
• What is the units digit of 2023²⁰²³?
• What is the value of the following expression, if x + 1/x = 2?

• Each dimension of a rectangular box is an integer number of inches. The volume of the box is 2023 in³. What is the minimum possible surface area of the box?
• What is the maximum possible product for a set of positive integers that have a sum of 2023?

Year-End Puzzle

There’s a math puzzle that’s been making its rounds on the web with the following proclamation:

82 beers minus your age plus $40 is the year you were born!

Of course, it gets way more interesting on the web, where you’ll find images of beer:

Don’t even get me started about the grammar and punctuation. (Why is “Beers” capitalized? And “your”? Ugh.)

You’ll also find pretty colors and clip art of beer mugs:

I’m also going to ignore the nonsensical nature of misaligned units — beers, years, and dollars? WTF?

But I won’t ignore the math. When the puzzle is shared online, it’s often accompanied by expressions of amazement — “OMG! This is amazing!” — or statements about its veracity — “This always works!” And it’s the latter claim that’s worth investigating.

To begin, I’ll show that this equation does, in fact, hold for me. I was born in 1971, and I’m 51 years old:

82 – 51 + 40 = 71

So far, so good.

But my friend Mike turns 51 on Friday. So he tried it:

82 – 50 + 40 = 72

Uh-oh. He was born on December 23, 1971, not 1972. It didn’t work for Mike; in fact, it won’t work for anyone who hasn’t had their birthday this year. Luckily, it’s late December, so this only excludes about 3% of the population; but in the US alone, that’s about 9 million people.

Separately, a version of this trick was texted to my sons, who are 15‎‑year‑old twins. They tried it:

82 – 15 + 40 = 107

Nope! They were born in 2007. Granted, the result of 107 means 107 years after 1900. But that’s inconsistent with the result being the last two digits of the year, so I’m not accepting it. In fact, this trick won’t work for anyone who wasn’t born in the 1900s. The graph of age distribution below — females on the left, males on the right — shows that approximately 90 million people were born in the year 2000 or later (age 22 or younger on the graph below). Of course, about 3% of them (3 million) were already counted above — those are the people who haven’t had birthdays this year and are too young for the trick to work. Which means that this trick doesn’t work for about 13 + 90 – 3 = 100 million people. And that’s just in the US.

Population Distribution of the United States [USA Facts]

So let’s say you know someone who was born in the 1900s and who has celebrated a birthday this year. Well, you could share this trick with them… but, you better do it soon! This trick won’t work once the calendar flips to 2023. (You could, of course, modify and start the trick with 83 beers or subtract 39, and then it’ll be fine. Though it’ll still only apply to people born in the 1900s who’ve already had their birthdays, and those people will be a little harder to find in January.)

This trick requires so many caveats, it hardly seems worth sharing, right? Well, not if you’re a math teacher and especially if you’re a secondary math teacher. Above, we dabbled in a little set theory with the principle of inclusion and exclusion while considering

(people born in the 1900s) ∪ (people who’ve had birthdays this year).

It can also lead to a good discussion of domain and range. The function y(a), where y is the year based on your age, a, can be simplified as:

y(a) = 82 – a + 40 = 122 – a

A restriction on the domain of 22 < a < 122 allows the trick to work just fine. And from a practical standpoint, the restriction that a < 122 is probably unnecessary. Lucille Randon is currently the oldest person in the world at 118 years of age, so unless you plan to share the trick with a giant tortoise or a bristlecone pine tree, you’re probably okay.

But I don’t want to leave you like that, so here’s a math trick that will always work.

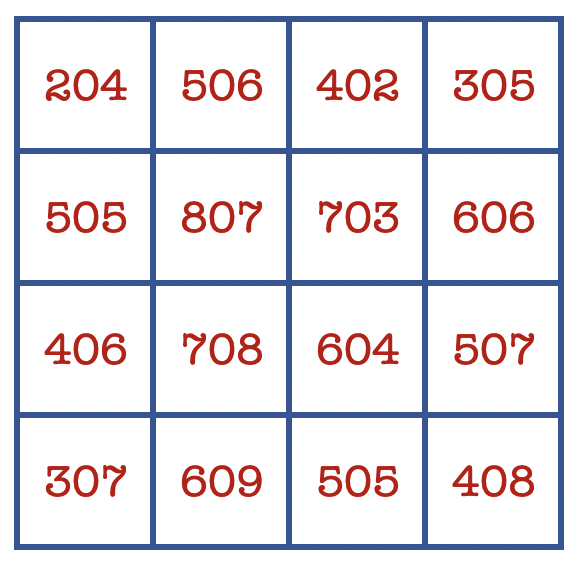
1. In the grid below, circle any number. Then, cross out the other numbers in the same row or column. (For instance, if you circled the 204 in the upper left cell, you’d then cross out 506, 402, and 305 in the top row as well as 505, 406, and 307 in the left column.)
2. Circle one of the remaining nine numbers, and again cross out the other numbers in the same row or column.
3. Circle one of the remaining four numbers, then cross out the other numbers in the same row or column.
4. This should leave just one number. Circle it.
5. At this point, one number should be circled in each row and column. If that’s not the case, start over at Step 1. If that is the case, though, good job! Find the sum of the four circled numbers.

I obviously have no idea which four numbers you selected. But I do know that the sum you obtained was 2023. (Now would be an appropriate time for applause. But that may be a little awkward if you’re reading this at work and folks in neighboring cubicles are within earshot.)

I know, it feels like magic. But it’s not; it’s just math.

Happy holidays, and happy new year!

Push-Up Percentages

Hands down, push-ups are my favorite exercise!

If you’re friends with me on Facebook, then you know I’m raising money for St. Jude Children’s Hospital by participating in the St. Jude Push-Up Challenge. And if not, then let me tell you: I’m challenging myself to do 3,000 6,000 push-ups during the month of November. As of November 20, I was just 660 push-ups away from reaching my goal; you can see all of my progress on this Google sheet.

What’s been most fun about this challenge, though, is the math of it all. (Isn’t that always the case?)

Arithmetic. How many push-ups will I have to average each day to reach my goal? November has 30 days, and 6000 ÷ 30 = 200.

Logistics. How should I break up those 200 push‑ups each day? A regimented person might do 10 push‑ups a minute for 20 minutes, or maybe 25 push‑ups every hour for 8 hours. For the record, I’m not that routinized. Most days, I do anywhere from 8‑12 sets, with anywhere from 10 to 50 push‑ups per set. Though I did have one day — November 13 — where I set a timer and did 10 push‑ups every 45 seconds for 90 minutes; I completed 1,235 push‑ups that afternoon, a personal record for push‑ups in day.

Physics. When doing a push‑up, how much of your bodyweight are you actually moving? I know that I’m not pushing up all 200 pounds of my weight when doing a push‑up. And I’m sure the percentage decreases more as I elevate my hands. This is only a hypothesis, but incline push‑ups sure seem easier — I can do more of them before reaching failure — than regular push‑ups, and decline push‑ups seem harder. As it turns out, Jane Reaction explained exactly why this is in a Physics of Fitness Friday blog post, and her conclusions about the percent bodyweight supported by the hands when doing a push‑up were as follows:

• Regular Push-Up: 64%
• Incline Push-Up, Hands Raised 12″: 55%
• Decline Push-Up, Feet Raised 12″: 70%
• Decline Push-Up, Feet Raised 24″: 74%
• Handstand Push-Up: 100%

These, of course, are estimates, and Jane used her body for the calculations. The exact percentage will differ person to person, depending on your weight, the length of your arms, your body shape, the location of your center of mass, and other factors. For a reasonable estimate, Jane suggests placing your hands on a scale while in push‑up position, then dividing by your standing weight (i.e., your weight when standing on a scale). For instance, if your scale shows 128 pounds for your hands in push‑up position and 200 pounds when you stand on it — which is exactly what it showed for me — then your hands are supporting 128 ÷ 200 = 0.64, or 64%, of your bodyweight when doing a push‑up.

The following graph, from Zatsiorsky’s Science and Practice of Strength Training, shows the percent body weight based on the height that your feet or hands are elevated:

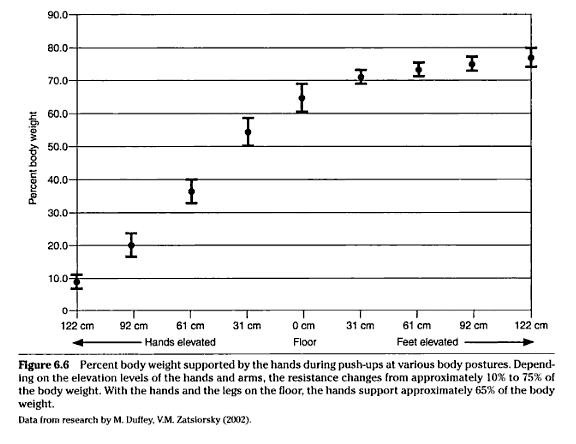
There were two reasons I was so curious about this estimate. First, math is cool. Second, I get bored easily, and I was wanting to substitute some bench presses for push-ups occasionally. Based on what’s above, I figured that if I did bench press with 125 pounds, then one rep would be equivalent to one push‑up. So on two of the days, I did a chest workout that included bench press, incline press, cable flyes… and then some push‑ups. And, yes, I was sore as hell the next day! But I was also rejuventated since I got to incorporate some activity other than just push‑ups.

I’m proud that, at 51 years of age, I’m going to complete this challenge. But I’m even more proud that I’m raising money for a good cause. If you’d like to contribute to St. Jude, visit my Donate page on Facebook. And if not, no worries; here’s one more joke for you before you go…

A man in a bar offers $100 to anyone who can do 100 push‑ups. Another patron leaves for a few minutes, then returns and says, “I’ll take that bet!” He drops to the ground and does 30 easily but then starts slowing down around 40 and collapses before he reaches 50. “I don’t understand,” he says. “I just did 150 outside!”